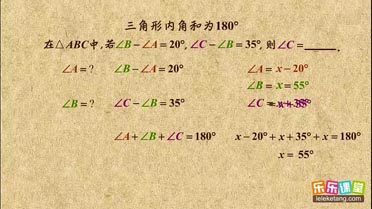三角形按边分类介绍:
1. 利用三边关系确定等腰三角形第三边的长度。
三角形的三边关系介绍:
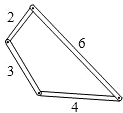
1. 三角形三边关系:三角形任意两边之和大于第三边;
2. 三角形三边关系的应用:在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形。
利用三边关系计数介绍:
1. 与三角形三边关系有关的计数问题。
三角形按角度分类介绍:
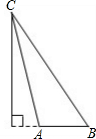
1. 锐角三角形:三个角都是锐角的三角形;
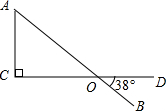
2. 直角三角形:有一个角是直角的三角形;
3. 钝角三角形:有一个角是钝角的三角形。
三角形内角和求角介绍:
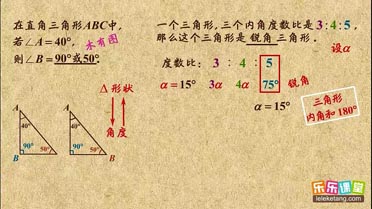
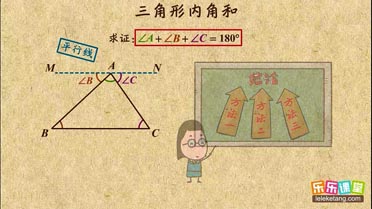
1. 三角形内角和定理:三角形内角和是180°;
2. 三角形内角和定理的应用:
①直接根据两已知角求第三个角;
②依据三角形中角的关系,用代数方法求三个角;
③在直角三角形中,已知一锐角可利用两锐角互余求另一锐角。
三角形内角和之列方程介绍:
1. 利用列方程的技巧处理三角形内角度计算问题。
待删除介绍:
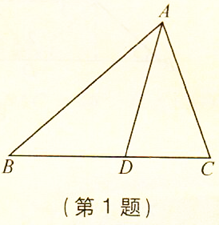
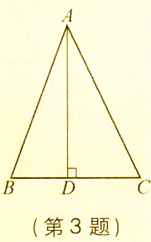
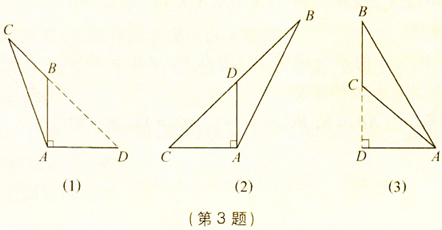
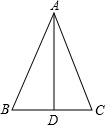
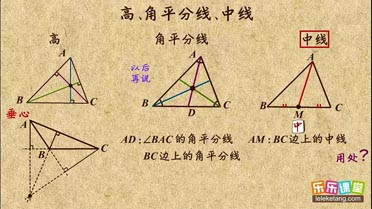
1. 三角形的高:从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高;
2. 三角形的角平分线:三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线;
3. 三角形的中线:三角形一边的中点与此边所对顶点的连线叫做三角形的中线。
········ THE END ········
三角形中的边角关系
下一节:
命题与证明
返回乐学堂首页