


| 1 |
| 2 |
| 1 |
| 2 |


| 180°-100° |
| 2 |

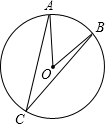
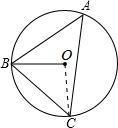 解:连接OC.
解:连接OC.| 180-100 |
| 2 |

| 1 |
| 2 |
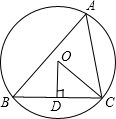
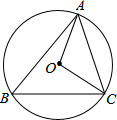
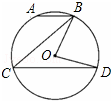
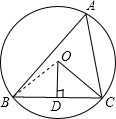 解:连接OB,
解:连接OB,| 180°-∠BOC |
| 2 |


| 1 |
| 2 |
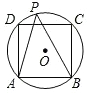
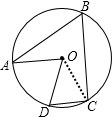
 解:连接OA,OB.根据正方形的性质,得∠AOB=90°.再根据圆周角定理,得∠APB=45°.
解:连接OA,OB.根据正方形的性质,得∠AOB=90°.再根据圆周角定理,得∠APB=45°.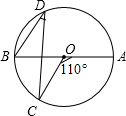
| 1 |
| 2 |
| 1 |
| 2 |





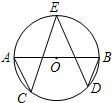
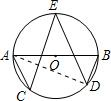 解:连接AD,
解:连接AD,


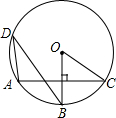
| 1 |
| 2 |
| 1 |
| 2 |


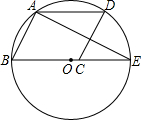


| 1 |
| 2 |
| 1 |
| 2 |

 解:连接OE,
解:连接OE,
| 1 |
| 2 |



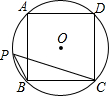
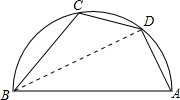
 解:连接BD,
解:连接BD,| AD+BC |
| 2 |
| 1 |
| 2 |
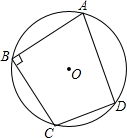
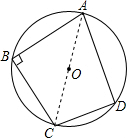 解:连接AC,
解:连接AC,



| 1 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 解:如图,在⌒AD上取点M,连接AM,CM,
解:如图,在⌒AD上取点M,连接AM,CM,
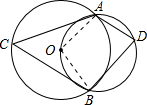 解:连OA,OB,如图,
解:连OA,OB,如图,| 1 |
| 2 |

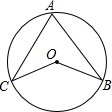
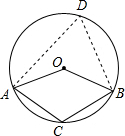 解:∵∠AOB=2∠ADB,∠AOB=130°,
解:∵∠AOB=2∠ADB,∠AOB=130°,| 1 |
| 2 |
| 1 |
| 2 |

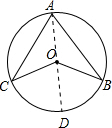
 解:在优弧⌒ADC上取点D,连接AD,CD,
解:在优弧⌒ADC上取点D,连接AD,CD,| 1 |
| 2 |
| 1 |
| 2 |
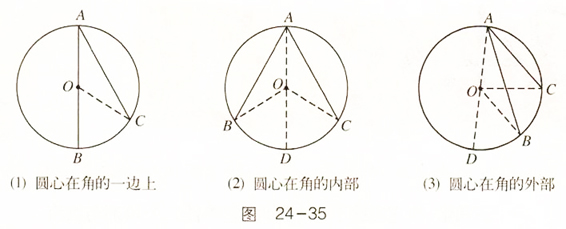
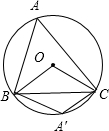 解:当△ABC为锐角三角形,即点A在优弧BC上,则∠A=
解:当△ABC为锐角三角形,即点A在优弧BC上,则∠A=| 1 |
| 2 |
| 1 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |







































| 1 |
| 2 |


| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |





