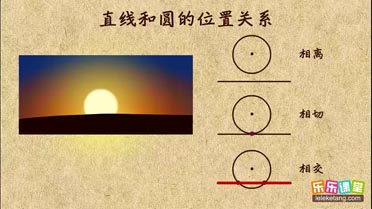
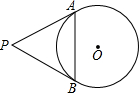直线和圆的位置关系介绍:
1. 直线与圆的位置关系:
①相离:一条直线和圆没有公共点;
②相切:一条直线和圆只有一个公共点;
③相交:一条直线和圆有两个公共点;
2. 设⊙O的半径为r,圆心O到直线l的距离为d。直线与圆位置关系:
①直线l和⊙O相交时d<r;
②直线l和⊙O相切时d=r;
③直线l和⊙O相离时d>r。
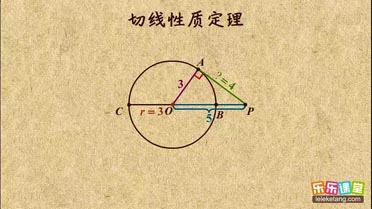
切线性质定理介绍:
1. 切线性质定理:
①圆的切线垂直于经过切点的半径;
②经过圆心且垂直于切线的直线必经过切点;
③经过切点且垂直于切线的直线必经过圆心;
2. 切线性质的运用:由定理可知,若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系。
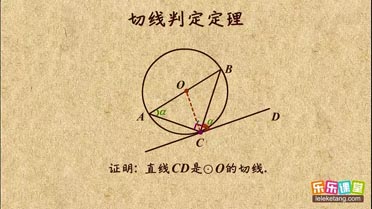
切线判定定理介绍:
1. 切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线;
2. 在应用判定定理时注意:
①切线必须满足两个条件:1)经过半径的外端;2)垂直于这条半径,否则就不是圆的切线;
②切线的判定定理实际上是从“圆心到直线的距离等于半径时,直线和圆相切”这个结论直接得出来的。
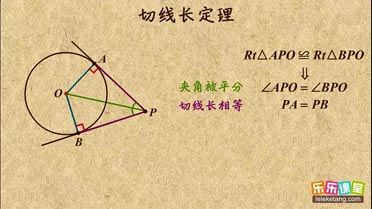
切线长定理介绍:
1. 切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角;
2. 切线长定理包含着一些隐含结论:
①垂直关系三处;
②全等关系三对;
③弧相等关系两对,在一些证明求解问题中经常用到。
········ THE END ········
直线与圆的位置关系、三角形的内切圆
下一节:
正多边形与圆
返回乐学堂首页





 解:根据题意画出图象,假设以A为圆心与BC相切于点D,
解:根据题意画出图象,假设以A为圆心与BC相切于点D,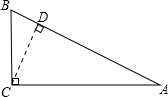

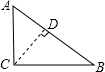


 解:连接OD,
解:连接OD,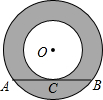
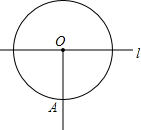
 解:设AB于小圆切于点C,连接OC,OB.
解:设AB于小圆切于点C,连接OC,OB.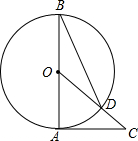

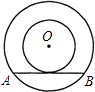
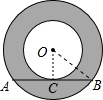
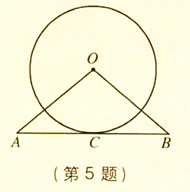
 解:过O作OC⊥AB于C,连OA,如图,
解:过O作OC⊥AB于C,连OA,如图,

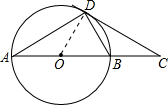 解:如图,连接OD,
解:如图,连接OD,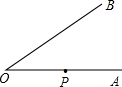
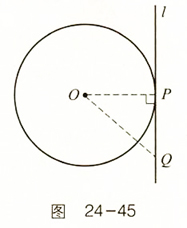
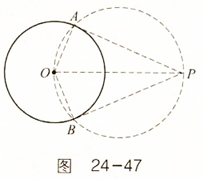
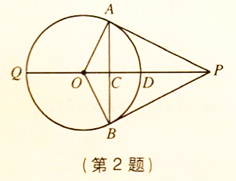
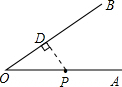 解:作PD⊥OB于D.
解:作PD⊥OB于D.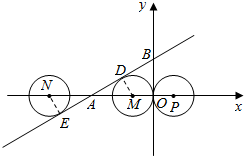 解:如图所示,∵点P的坐标为(1,0),⊙P与y轴相切于点O,
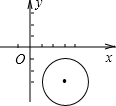
解:如图所示,∵点P的坐标为(1,0),⊙P与y轴相切于点O,
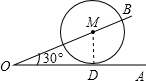 解:当⊙M与OA相切时,MB=r,∠MDO=90°;
解:当⊙M与OA相切时,MB=r,∠MDO=90°;
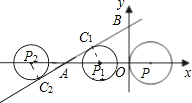 解:∵直线y=
解:∵直线y=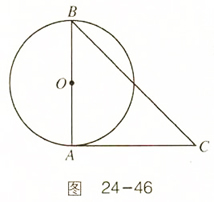

 解:方法一:
解:方法一: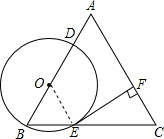

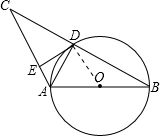

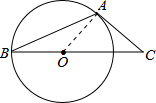
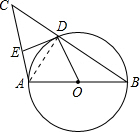 解:当AB=AC时,如图:连接AD,
解:当AB=AC时,如图:连接AD,




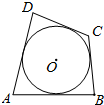
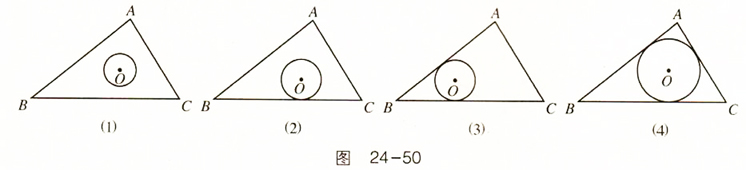 如图24 - 50,⊙O按其位置与三角形的边是否相切分四种情形:图24-50(1)的⊙O与三边都不相切,图24 - 50(2)的⊙O只与一边相切,图24 - 50(3)的⊙O与两边相切,图24 - 50(4)的⊙O与三边都相切.
如图24 - 50,⊙O按其位置与三角形的边是否相切分四种情形:图24-50(1)的⊙O与三边都不相切,图24 - 50(2)的⊙O只与一边相切,图24 - 50(3)的⊙O与两边相切,图24 - 50(4)的⊙O与三边都相切.

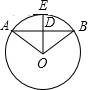
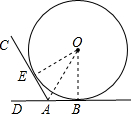 连接OE、OA、OB,
连接OE、OA、OB,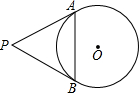




































 如图24 - 50,⊙O按其位置与三角形的边是否相切分四种情形:图24-50(1)的⊙O与三边都不相切,图24 - 50(2)的⊙O只与一边相切,图24 - 50(3)的⊙O与两边相切,图24 - 50(4)的⊙O与三边都相切.
如图24 - 50,⊙O按其位置与三角形的边是否相切分四种情形:图24-50(1)的⊙O与三边都不相切,图24 - 50(2)的⊙O只与一边相切,图24 - 50(3)的⊙O与两边相切,图24 - 50(4)的⊙O与三边都相切.