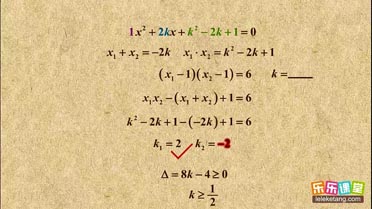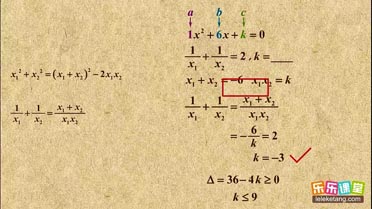我的课件 视频下载 我的作业 我的班级 我的学情 使用指南
立即申请，享受乐学堂完整版
老师申请:
所在地：
选择学校：
未找到您所在的学校？请加入乐乐课堂教师群反馈。
学校人数：
QQ邮箱：
@qq.com
申请成功后，我们将发送邀请码到您的QQ邮箱。
温馨提示
1. 申请成为老师，才可以享受乐学堂完整版；
2. 审核会在一个工作日内完成，审核结果会发送到您的QQ邮箱；
3. 如有任何问题，可以扫描二维码加入乐乐课堂教师群进行咨询；
4. 暂时不接受学生/家长申请，如有兴趣请访问乐乐课堂官网。
申请使用乐学堂完整版
申请成功
亲爱的老师
审核结果将在一个工作日内发送至您的QQ邮箱。
您也可以加入乐乐课堂教师群（836985968），即时了解审核进展。
乐乐课堂教师群
申请已通过
请到QQ邮箱中查收邮件完成注册
特殊考点
利用方程根的概念求值介绍：

1. 所谓方程的根，一定满足代入方程后能使方程成立；所以看到题目提到方程的根，就把根代入方程。
若关于x的一元二次方程x2+3x+a=0有一个根是-1，则a=    ．
分析把x=-1代入原方程，列出关于a的新方程，通过解新方程可以求得a的值．
解答∵关于x的一元二次方程x2+3x+a=0有一个根是-1，
∴（-1）2+3×（-1）+a=0，
解得 a=2，
故答案为：2．
点评本题考查的是一元二次方程的根即方程的解的定义．一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．
若x=-2是关于x的一元二次方程x2-
5
2
ax+a2=0的一个根，则a的值为（　　）
  • A. 1或4
  • B. -1或-4
  • C. -1或4
  • D. 1或-4
分析将x=-2代入关于x的一元二次方程x2-
5
2
ax+a2=0，再解关于a的一元二次方程即可．
解答∵x=-2是关于x的一元二次方程x2-
5
2
ax+a2=0的一个根，
∴4+5a+a2=0，
∴（a+1）（a+4）=0，
解得a1=-1，a2=-4，
故选：B．
点评本题主要考查了一元二次方程的解的定义，解题关键是把x的值代入，再解关于a的方程即可．
已知关于x的方程x2+2x+k=0的一个根是-1，则k=    ．
分析将x=-1代入已知方程，列出关于k的新方程，通过解新方程即可求得k的值．
解答根据题意，得
（-1）2+2×（-1）+k=0，
解得k=1；
故答案是：1．
点评本题考查的是一元二次方程的根即方程的解的定义．一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．
关于x的方程x2+mx-2m2=0的一个根为1，则m的值为（　　）
  • A. 1
  • B.
    1
    2
  • C. 1或
    1
    2
  • D. 1或-
    1
    2
分析根据关于x的方程x2+mx-2m2=0的一个根为1，可将x=1代入方程，即可得到关于m的方程，解方程即可求出m值．
解答解：把x=1代入方程可得1+m-2m2=0，
∴2m2-m-1=0，
m=
1±
√1+8
4
=
1±3
4
，
解得：m=1或-
1
2
．
故选：D．
点评此题主要考查了方程的解的意义和一元二次方程的解法．熟练运用公式法求得一元二次方程的解是解决问题的关键．
一元二次方程（a+1）x2-ax+a2-1=0的一个根为0，则a=    ．
分析根据一元二次方程的定义和一元二次方程的解的定义得到a+1≠0且a2-1=0，然后解不等式和方程即可得到a的值．
解答解：∵一元二次方程（a+1）x2-ax+a2-1=0的一个根为0，
∴a+1≠0且a2-1=0，
∴a=1．
故答案为1．
点评本题考查了一元二次方程的定义：含一个未知数，并且未知数的最高次数为2的整式方程叫一元二次方程，其一般式为ax2+bx+c=0（a≠0）．也考查了一元二次方程的解的定义．
关于x的一元二次方程（a-1）x2+x+|a|-1=0的一个根是0，则实数a的值为（　　）
  • A. -1
  • B. 0
  • C. 1
  • D. -1或1
分析先把x=0代入方程求出a的值，然后根据二次项系数不能为0，把a=1舍去．
解答把x=0代入方程得：
|a|-1=0，
∴a=±1，
∵a-1≠0，
∴a=-1．
故选A．
点评本题考查的是一元二次方程的解，把方程的解代入方程得到a的值，再由二次项系数不为0，确定正确的选项．
若关于x的一元二次方程ax2+bx+5=0（a≠0）的解是x=1，则2013-a-b的值是（　　）
  • A. 2018
  • B. 2008
  • C. 2014
  • D. 2012
分析将x=1代入到ax2+bx+5=0中求得a+b的值，然后求代数式的值即可．
解答解：∵x=1是一元二次方程ax2+bx+5=0的一个根，
∴a•12+b•1+5=0，
∴a+b=-5，
∴2013-a-b=2013-（a+b）=2013-（-5）=2018．
故选A．
点评此题主要考查了一元二次方程的解，解题的关键是把已知方程的根直接代入方程得到待定系数的方程即可求得代数式a+b的值．
已知x=1是一元二次方程x2-mx+n=0的一个根，则m2-2mn+n2的值为    ．
分析把x=1代入方程x2-mx+n=0求出n-m=-1，把m2-2mn+n2化成（n-m）2代入求出即可．
解答解：把x=1代入方程x2-mx+n=0得：1-m+n=0，
∴n-m=-1，
m2-2mn+n2=（n-m）2=（-1）2=1．
故答案为：1．
点评本题主要考查对一元二次方程的解，完全平方公式等知识点的理解和掌握，能求出n-m=-1和把m2-2mn+n2化成 （n-m）2是解此题的关键．
若x=1是关于x的一元二次方程x2+3mx+n=0的解，则6m+2n=    ．
分析先把x=1代入x2+3mx+n=0，得到3m+n=-1，再把要求的式子进行整理，然后代入即可．
解答解：把x=1代入x2+3mx+n=0得：
1+3m+n=0，
3m+n=-1，
则6m+2n=2（3m+n）=2×（-1）=-2；
故答案为：-2．
点评此题考查了一元二次方程的解，解题的关键是把x的值代入，得到一个关于m，n的方程，不要求m．n的值，要以整体的形式出现．
已知x=1是方程x2+mx+n=0的一个根，则代数式m2+2mn+n2的值为（　　）
  • A. -1
  • B. 1
  • C. -2
  • D. 2
分析把x=1代入方程x2+mx+n=0求出m+n=-1，根据完全平方公式代入求出即可．
解答解：把x=1代入方程x2+mx+n=0得：1+m+n=0，
∴m+n=-1，
m2+2mn+n2=（m+n）2=（-1）2=1，
故选B．
点评本题考查了完全平方公式和一元二次方程的解的应用，关键是求出m+n的值．
已知一个根求另一个根介绍：

1. 直接利用根与系数的关系，可以已知一元二次方程的一个根，求另一个根。
关于x的一元二次方程（m+1）x2-2mx=3的一个根是3，则另一个根等于    ．
分析根据方程根的定义，把x的值代入原方程求m，然后根据一元二次方程根与系数的关系求另一个根．
解答解：当x=3时，得9（m+1）-6m-3=0，
解得m=-2，原方程化为
x2-4x+3=0，
根据根与系数的关系，
得3x=3，x=1，即另一个根为1，
故填1．
点评本题考查了一元二次方程根与系数的关系和方程根的定义．此题需要根据解的定义先求出系数中的字母m的值，再求另一个根的值．
已知一元二次方程x2-6x+C=0有一个根为2，则另一根为（　　）
  • A. 2
  • B. 3
  • C. 4
  • D. 8
分析利用根与系数的关系来求方程的另一根．
解答设方程的另一根为α，则α+2=6，
解得α=4．
故选C．
点评本题考查了根与系数的关系．若二次项系数为1，常用以下关系：x1，x2是方程x2+px+q=0的两根时，x1+x2=-p，x1x2=q，反过来可得p=-（x1+x2），q=x1x2，前者是已知系数确定根的相关问题，后者是已知两根确定方程中未知系数．
已知方程x2-4x+m=0的一个根为-2，则m=    ，另一个根为    ．
分析根据根与系数的关系，可求出两根的和与两根的积，将已知的根代入即可求出另一根及m的值．
解答解：设原方程的两根为x1、x2；
则：x1+x2=4，x1x2=m；
∵x1=-2，
∴x2=4-x1=6，m=x1x2=-12；
即方程的另一根是6，m的值为-12．
点评此题主要考查的是一元二次方程根与系数的关系．
已知x=-2是方程x2+mx-6=0的一个根，则方程的另一个根是    ．
分析根据根与系数的关系得到-2•x1=-6，然后解一次方程即可．
解答解：设方程另一个根为x1，根据题意得-2•x1=-6，
所以x1=3．
故答案为3．
点评本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程两根为x1，x2，则x1+x2=-
b
a
，x1•x2=
c
a
．
已知x1=-1是方程x2+mx-5=0的一个根，则m=    ，另一个根为    ．
分析将x1=-1代入原方程，可求出m的值，进而可通过解方程求出另一根．
解答解：由题意得：（-1）2+（-1）×m-5=0，解得m=-4；
当m=-4时，方程为x2-4x-5=0
解得：x1=-1，x2=5
所以方程的另一根x2=5．
点评此题主要考查了一元二次方程解的意义，以及运用解的定义解决相关问题的能力．
已知根的个数求参数介绍：

已知含参一元二次方程根的情况求参数的原理是一元二次方程ax^2+bx+c=0（a≠0）的根与△=b^2-4ac有如下关系：
1. 当方程有两个不相等的两个实数根时，△＞0；
2. 当方程有两个相等的两个实数时，△=0；
3. 当方程无实数根时，△＜0。
已知关于x的一元二次方程x2+2x-a=0有两个相等的实数根，则a的值是（　　）
  • A. 4
  • B. -4
  • C. 1
  • D. -1
分析根据根的判别式的意义得到△=22-4•（-a）=0，然后解方程即可．
解答解：根据题意得△=22-4•（-a）=0，
解得a=-1．
故选D．
点评本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
关于x的一元二次方程x2-3x+m=0有两个不相等的实数根，则实数m的取值范围为（　　）
  • A. m＞
    9
    4
  • B. m＜
    9
    4
  • C. m=
    9
    4
  • D. m＜-
    9
    4
分析先根据判别式的意义得到△=（-3）2-4m＞0，然后解不等式即可．
解答根据题意得△=（-3）2-4m＞0，
解得m＜
9
4
．
故选：B．
点评本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
一元二次方程x2-2x+m=0总有实数根，则m应满足的条件是（　　）
  • A. m＞1
  • B. m=1
  • C. m＜1
  • D. m≤1
分析根据根的判别式，令△≥0，建立关于m的不等式，解答即可．
解答∵方程x2-2x+m=0总有实数根，
∴△≥0，
即4-4m≥0，
∴-4m≥-4，
∴m≤1．
故选：D．
点评本题考查了根的判别式，一元二次方程根的情况与判别式△的关系：
（1）△＞0⇔方程有两个不相等的实数根；
（2）△=0⇔方程有两个相等的实数根；
（3）△＜0⇔方程没有实数根．
已知关于x的一元二次方程x2+bx+b-1=0有两个相等的实数根，则b的值是    ．
分析根据方程有两个相等的实数根，得到根的判别式的值等于0，即可求出b的值．
解答解：根据题意得：△=b2-4（b-1）=（b-2）2=0，
则b的值为2．
故答案为：2
点评此题考查了根的判别式，根的判别式的值大于0，方程有两个不相等的实数根；根的判别式的值等于0，方程有两个相等的实数根；根的判别式的值小于0，方程没有实数根．
关于x的一元二次方程x2-3x+b=0有两个不相等的实数根，则b的取值范围是    ．
分析根据判别式的意义得到Δ=(-3)2-4b＞0，然后解不等式即可．
解答解：根据题意得Δ=(-3)2-4b＞0，
解得b＜
9
4
．
故答案为：b＜
9
4
．
点评本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式Δ=b2-4ac：当Δ＞0，方程有两个不相等的实数根；当Δ=0，方程有两个相等的实数根；当Δ＜0，方程没有实数根．
若关于x的方程x2-x+a=0有实数根，则a的值可以是（　　）
  • A. 2
  • B. 1
  • C. 0.5
  • D. 0.25
分析根据判别式的意义得到△=（-1）2-4a≥0，然后解不等式，最后根据不等式的解集进行判断．
解答解：根据题意得△=（-1）2-4a≥0，
解得a≤
1
4
．
故选D．
点评本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
若关于x的一元二次方程(k-1)x2+2x-2=0有不相等实数根，则k的取值范围是(　　)
  • A. k＞
    1
    2
  • B. k≥
    1
    2
  • C. k＞
    1
    2
    且k≠1
  • D. k≥
    1
    2
    且k≠1
分析根据判别式的意义得到△=22-4(k-1)×(-2)＞0，然后解不等式即可．
解答∵关于x的一元二次方程(k-1)x2+2x-2=0有不相等实数根，
∴△=22-4(k-1)×(-2)＞0，
解得k＞
1
2
；且k-1≠0，即k≠1．
故选：C．
点评此题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
关于x的一元二次方程kx2-4x-1=0有两个实根，则k的取值范围是(　　)
  • A. k≥-4
  • B. k≥4
  • C. k＞-4
  • D. k≥-4且k≠0
分析根据已知方程的根的情况来确定根的判别式Δ≥0，通过解不等式来求k的取值范围．
解答解：∵关于x的一元二次方程kx2-4x-1=0有两个实根，
∴Δ=(-4)2-4k•(-1)≥0，且k≠0，
解得，k≥-4且k≠0．
故选D．
点评本题考查了根的判别式，一元二次方程的定义．一元二次方程根的情况与判别式△的关系：
(1)Δ＞0⇔方程有两个不相等的实数根；
(2)Δ=0⇔方程有两个相等的实数根；
(3)Δ＜0⇔方程没有实数根．
若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根，则实数k的取值范围是（　　）
  • A. k＞-1
  • B. k＜1且k≠0
  • C. k≥-1且k≠0
  • D. k＞-1且k≠0
分析根据方程有两个不相等的实数根，得到根的判别式的值大于0列出不等式，且二次项系数不为0，即可求出k的范围．
解答解：∵一元二次方程kx2-2x-1=0有两个不相等的实数根，
∴△=b2-4ac=4+4k＞0，且k≠0，
解得：k＞-1且k≠0．
故选D
点评此题考查了一元二次方程根的判别式，根的判别式的值大于0，方程有两个不相等的实数根；根的判别式的值等于0，方程有两个相等的实数根；根的判别式的值小于0，方程没有实数根．
若关于x的方程ax2+2（a+2）x+a=0有实数解，那么实数a的取值范围是（　　）
  • A. a≥-1
  • B. a≤1
  • C. a＞-1
  • D. a＜1
分析当a=0时，方程是一元一次方程，方程的根可以求出，即可作出判断；
当a≠0时，方程是一元二次方程，只要有实数根，则应满足：△≥0，建立关于a的不等式，求得a的取值范围即可．
解答解：当a=0时，方程是一元一次方程，有实数根，
当a≠0时，方程是一元二次方程，
若关于x的方程ax2+2（a+2）x+a=0有实数解，
则△=[2（a+2）]2-4a•a≥0，
解得：a≥-1．
故答案为：A．
点评此题考查了根的判别式，注意本题分a=0与a≠0两种情况讨论是解决本题的关键．并且利用了一元二次方程若有实数根则应有△≥0．
证明方程恒有实根介绍：

1. 证明含参一元二次方程恒有实根就是证明判别式恒大于等于0。
试证明：不论m为何值，方程2x2+3(m-1)x+m2-4m-7=0总有两个不相等的实数根．
分析利用根的判别式列出关于方程系数的代数式，通过配方法化为完全平方式来判断△的正负，从而证明方程有两个不相等的实数根．
解答证明：∵Δ=[-3(m-1)]2-4×2×(m2-4m-7)=(m+7)2+16＞0
∴有两个不相等的实数根．
点评本题考查了一元二次方程根的判别式的应用．解题关键是把判别式△转化成完全平方式与一个正数的和的形式，才能判断出它的正负性．
已知关于x的方程x2-2kx+（2k-1）=0，其判别式可以化成m（k+a）2+b的形式，所以方程有两个不同的实根。则a+b=    ．
分析表示出根的判别式，进行配方后得到完全平方式，进行解答．
解答解：∵△=4k2-4（2k-1）=4（k-1）2，
∴a=-1，b=0，
故a+b=-1
点评本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）的根的判别式△=b2-4ac．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
整数根之判别式介绍：

1. 利用根的判别式解一元二次方程整数根问题的原理是直接利用判别式得到不等式，然后求出参数的范围，再在范围内枚举满足条件的即可。
当m是什么整数时，关于x的一元二次方程mx2-4x+4=0与x2-4mx+4m2-4m-5=0的解都是整数？
分析这两个一元二次方程都有解，因而根与判别式△≥0，即可得到关于m不等式，从而求得m的范围，再根据m是整数，即可得到m的可能取到的几个值，然后对每个值进行检验，是否符合使两个一元二次方程的解都是整数即可确定m的值．
解答解：∵关于x的一元二次方程mx2-4x+4=0与x2-4mx+4m2-4m-5=0有解，
对mx2-4x+4=0，
∴m≠0，△=16-16m≥0，即m≤1且m≠0；
x2-4mx+4m2-4m-5=0，
△=16m2-16m2+16m+20≥0，
∴4m+5≥0，m≥-
5
4
；
∴-
5
4
≤m≤1，而m是整数，
所以m=1，m=0（舍去），m=-1
当m=1时，mx2-4x+4=0即x2-4x+4=0，方程的解是x1=x2=2；
x2-4mx+4m2-4m-5=0即x2-4x-5=0，方程的解是x1=5，x2=-1；
当m=-1时，mx2-4x+4=0变为-x2-4x+4=0，它的解不是整数，不符合题意．
故m=1．
点评解答此题要知道一元二次方程根的情况与判别式△的关系，首先根据根的判别式确定m的范围是解决本题的关键．
关于x的一元二次方程（k-3）x2-3x+2=0有两个不相等的实数根．若方程的两根均为整数，则正整数k=    ．
分析首先由于一元二次方程有两个不相等的实数根，则可知k-3≠0，△＞0，公共部分就是k的取值范围．
再通过k的取值范围确定出k的正整数值，依次代入求出一元二次方程的解，满足两根都是整数就可以．
解答解：∵方程有两个不相等的实数根，∴
{
(-3)2-4×2(k-3)>0.
k-3≠0.

解得，k＜
33
8
且k≠3．
∴k的正整数值为1、2、4
如果k=1，原方程为-2x2-3x+2=0．
解得x1=-2，x2=
1
2
，不符合题意，舍去．
如果k=2，原方程为-x2-3x+2=0，
解得x1=
-3+
√17
2
，x2=
-3-
√17
2
，不符合题意，舍去．
如果k=4，原方程为x2-3x+2=0，解得x1=1，x2=2，符合题意．
∴k=4．
点评这道题主要考查一元二次方程的根的判别式，熟知一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac的关系是解答此题的关键．
整数根之直接求根介绍：

1. 直接解出含参方程解含参一元二次方程的整数根问题。
关于x的一元二次方程mx2-（3m+2）x+2m+2=0．当m=    时，此方程的两个根都为正整数．
分析表示出根的判别式，得到根的判别式大于0，进而确定出方程总有两个不相等的实数根；利用求根公式表示出方程的两根：x1=1，x2=2+
2
m
，要使原方程的根是整数，必须使得
x2=2+
2
m
为正整数．
解答解：∵△=b2-4ac=△=[-（3m+2）]2-4m（2m+2）=m2+4m+4=（m+2）2，
∴x=
2m+2
m
或x=1，
∵
2m+2
m
=2+
2
m
，m＞0，
∴
2m+2
m
=2+
2
m
＞2，
∵x1＜x2，
∴x1=1，x2=2+
2
m
，
∵m为整数，
∴m只能取±1，±2，
又∵根为正整数
∴m只能取1，±2
点评此题考查了根的判别式，以及求根公式，根的判别式的值大于0，方程有两个不相等的实数根；根的判别式的值等于0，方程有两个相等的实数根；根的判别式的值小于0，方程没有实数根．
已知关于x的方程mx2-（m+2）x+2=0（m≠0）．当正整数m=    或    （从小到大依次填写）时，此方程的两个根都为整数．
分析先计算判别式的值得到△=（m+2）2-4m×2=（m-2）2，再根据非负数的值得到△≥0，然后利用因式分解法解方程得到x1=1，x2=
2
m
，然后利用整数的整除性确定正整数m的值．
解答解：∵m≠0，
△=（m+2）2-4m×2
=m2-4m+4
=（m-2）2，
而（m-2）2≥0，即△≥0，
∴方程总有两个实数根；

（x-1）（mx-2）=0，
x-1=0或mx-2=0，
∴x1=1，x2=
2
m
，
当m为正整数1或2时，x2为整数，
即方程的两个实数根都是整数，
∴正整数m的值为1或2．
点评本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
已知两根的和与积求参数介绍：

1. 掌握已知两根的和与积求参数问题的解题技巧。
已知一元二次方程的两根分别是2和-3，则这个一元二次方程是（　　）
  • A. x2-6x+8=0
  • B. x2+2x-3=0
  • C. x2-x-6=0
  • D. x2+x-6=0
分析首先设此一元二次方程为x2+px+q=0，由二次项系数为1，两根分别为2，-3，根据根与系数的关系可得p=-（2-3）=1，q=（-3）×2=-6，继而求得答案．
解答设此一元二次方程为x2+px+q=0，
∵二次项系数为1，两根分别为2，-3，
∴p=-（2-3）=1，q=（-3）×2=-6，
∴这个方程为：x2+x-6=0．
故选：D．
点评此题考查了根与系数的关系．此题难度不大，注意若二次项系数为1，x1，x2是方程x2+px+q=0的两根时，x1+x2=-p，x1x2=q，反过来可得p=-（x1+x2），q=x1x2．
若方程x2+（m2-1）x+m=0的两根互为相反数，则m的值为（　　）
  • A. 1或-1
  • B. 1
  • C. 0
  • D. -1
分析因为方程x2+（m2-1）x+m=0的两根互为相反数，所以m2-1=0，由此求出m，然后代入判别式中检验即可求出m的值．
解答解：∵方程x2+（m2-1）x+m=0的两根互为相反数，
∴x1+x2=-
b
a
=0
∴m2-1=0，
解得m=±1，
∵互为相反数的积小于等于0，即m≤0，
∴m=-1．
故选D．
点评本题主要考查了根与系数的关系和相反数的定义．要会灵活运用各种方法，巧妙解题．两根互为相反数，隐含的条件是，两根之和等于零，两根之积小于或等于零．
方程x2-（m+6）x+m2=0有两个相等的实数根，且满足x1+x2=x1x2，则m的值是（　　）
  • A. -2或3
  • B. 3
  • C. -2
  • D. -3或2
分析根据根与系数的关系有：x1+x2=m+6，x1x2=m2，再根据x1+x2=x1x2得到m的方程，解方程即可，进一步由方程x2-（m+6）+m2=0有两个相等的实数根得出b2-4ac=0，求得m的值，由相同的解解决问题．
解答∵x1+x2=m+6，x1x2=m2，x1+x2=x1x2，
∴m+6=m2，
解得m=3或m=-2，
∵方程x2-（m+6）x+m2=0有两个相等的实数根，
∴△=b2-4ac=（m+6）2-4m2=-3m2+12m+36=0
解得m=6或m=-2
∴m=-2．
故选：C．
点评本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）根的判别式△=b2-4ac．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．同时考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程的两根为x1，x2，则x1+x2=-
b
a
，x1•x2=
c
a
．
若关于x的一元二次方程x2+bx+c=0的两个实数根分别为x1=-2，x2=4，则b+c的值是（　　）
  • A. -10
  • B. 10
  • C. -6
  • D. -1
分析根据根与系数的关系得到-2+4=-b，-2×4=c，然后可分别计算出b、c的值，进一步求得答案即可．
解答∵关于x的一元二次方程x2+bx+c=0的两个实数根分别为x1=-2，x2=4，
∴根据根与系数的关系，可得-2+4=-b，-2×4=c，
解得b=-2，c=-8
∴b+c=-10．
故选：A．
点评此题考查根与系数的关系，解答此题的关键是熟知一元二次方程根与系数的关系：x1+x2=-
b
a
，x1x2=
c
a
．
关于x的一元二次方程x2+（k2-4）x+k+1=0的两实数根互为相反数，则k的值是（　　）
  • A. 2
  • B. 0
  • C. ±2
  • D. -2
分析首先根据一元二次方程x2+（k2-4）x+k+1=0的两实数根互为相反数，得k2-4=0，即k=±2；再进一步代入看方程是否有实数根．
解答解：∵一元二次方程x2+（k2-4）x+k+1=0的两实数根互为相反数，
∴-（k2-4）=0，即k=±2．
当k=2时，有方程x2+3=0，此方程无实数根，应舍去，取k=-2．
故选D．
点评此题要结合互为相反数的两个数的和为0以及一元二次方程根与系数的关系求得k的值，最后不要忘记代入检查方程是否有实数根．
关于x的方程ax2-(3a+1)x+2(a+1)=0有两个不相等的实根x1、x2，且有x1-x1x2+x2=1-a，则a的值是(　　)
  • A. 1
  • B. -1
  • C. 1或-1
  • D. 2
分析根据根与系数的关系得出x1+x2=-
b
a
，x1x2=
c
a
，整理原式即可得出关于a的方程求出即可．
解答解：依题意△＞0，即(3a+1)2-8a(a+1)＞0，
即a2-2a+1＞0，(a-1)2＞0，a≠1，
∵关于x的方程ax2-(3a+1)x+2(a+1)=0有两个不相等的实根x1、x2，且有x1-x1x2+x2=1-a，
∴x1-x1x2+x2=1-a，
∴x1+x2-x1x2=1-a，
∴
3a+1
a
-
2a+2
a
=1-a，
解得：a=±1，又a≠1，
∴a=-1．
故选：B．
点评此题主要考查了根与系数的关系，由x1-x1x2+x2=1-a，得出x1+x2-x1x2=1-a是解决问题的关键．
关于x的一元二次方程x2+2x+k+1=0的两个实根x1，x2，满足x1+x2-x1x2＜-1，则k的取值范围在数轴上表示为（　　）
  • A.
  • B.
  • C.
  • D.
分析根据根的判别式和根与系数的关系列出不等式，求出解集．
解答∵关于x的一元二次方程x2+2x+k+1=0有两个实根，
∴△≥0，
∴4-4（k+1）≥0，
解得k≤0，
∵x1+x2=-2，x1•x2=k+1，
∴-2-（k+1）＜-1，
解得k＞-2，
不等式组的解集为-2＜k≤0，
在数轴上表示为：
，
故选：D．
点评本题考查了根的判别式、根与系数的关系，在数轴上找到公共部分是解题的关键．
关于x的一元二次方程x2+2（m-1）x+m2=0的两个实数根分别为x1，x2，且x1+x2＞0，x1x2＞0，则m的取值范围是（　　）
  • A. m≤
    1
    2
  • B. m≤
    1
    2
    且m≠0
  • C. m＜1
  • D. m＜1且m≠0
分析先由根的判别式可得方程有两个实数根则△≥0，根据根与系数的关系得出x1+x2=-2（m-1），x1x2=m2，再由x1+x2＞0，x1x2＞0，解出不等式组即可．
解答∵△=[2（m-1）]2-4m2=-8m+4≥0，
∴m≤
1
2
，
∵x1+x2=-2（m-1）＞0，x1x2=m2＞0
∴m＜1，m≠0
∴m≤
1
2
且m≠0．
故选：B．
点评此题考查了根的判别式和根与系数的关系，一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根；（2）△=0⇔方程有两个相等的实数根；（3）△＜0⇔方程没有实数根，根与系数的关系是x1+x2=-
b
a
，x1x2=
c
a
．
两根平方和介绍：

1. 根与系数关系的应用技巧。
已知m，n是关于x的一元二次方程x2-3x+a=0的两个解，若（m-1）（n-1）=-6，则a的值为（　　）
  • A. -10
  • B. 4
  • C. -4
  • D. 10
分析利用根与系数的关系表示出m+n与mn，已知等式左边利用多项式乘多项式法则变形，将m+n与mn的值代入即可求出a的值．
解答根据题意得：m+n=3，mn=a，
∵（m-1）（n-1）=mn-（m+n）+1=-6，
∴a-3+1=-6，
解得：a=-4．
故选C
点评此题考查了根与系数的关系，熟练掌握根与系数的关系是解本题的关键．
已知一元二次方程x2-2x-2010=0的两根分别是x1和x2，则（1-x1）（1-x2）=    ．
分析利用一元二次方程根与系数的关系得到x1+x2和x1x2的值，然后把它们的值代入代数式可以求出代数式的值．
解答解：∵x1，x2是方程x2-2x-2010=0的两个根，
∴x1+x2=2，x1x2=-2010，
（1-x1）（1-x2）=x1x2-（x1+x2）+1=-2010-2+1=-2011．
故答案为：-2011．
点评本题考查的是一元二次方程的根与系数的关系，利用根与系数的关系求出两根的和与两根的积，然后把两根的和与两根的积代入代数式求出代数式的值．
已知m、n是方程x2+2
√2
x+1=0的两根，则代数式
√m2+n2+3mn
的值为（　　）
  • A. 9
  • B. ±3
  • C. 3
  • D. 5
分析根据一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系得到m+n=-2
√2
，mn=1，再变形
√m2+n2+3mn
得
√(m+n)2+mn
，然后把m+n=-2
√2
，mn=1整体代入计算即可．
解答解：∵m、n是方程x2+2
√2
x+1=0的两根，
∴m+n=-2
√2
，mn=1，
∴
√m2+n2+3mn
=
√(m+n)2+mn
=
√(-2
√2
)2+1
=
√9
=3．
故选C．
点评本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程两根分别为x1，x2，则x1+x2=-
b
a
，x1•x2=
c
a
．也考查了二次根式的化简求值．
方程x2+2kx+k2-2k+1=0的两个实数根x1，x2满足x
2
1
+x
2
2
=4，则k的值为    ．
分析由x
2
1
+x
2
2
=x
2
1
+2x1•x2+x
2
2
-2x1•x2=（x1+x2）2-2x1•x2=4，然后根据根与系数的关系即可得到一个关于k的方程，从而求得k的值．
解答解：∵方程x2+2kx+k2-2k+1=0的两个实数根，
∴△=4k2-4（k2-2k+1）≥0，
解得 k≥
1
2
．
∵x
2
1
+x
2
2
=4，
∴x
2
1
+x
2
2
=x
2
1
+2x1•x2+x
2
2
-2x1•x2=（x1+x2）2-2x1•x2=4，
又∵x1+x2=-2k，x1•x2=k2-2k+1，
代入上式有4k2-2（k2-2k+1）=4，
解得k=1或k=-3（不合题意，舍去）．
故答案为：1．
点评本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系： 若方程的两根为x1，x2， 则x1+x2=-
b
a
，x1•x2=
c
a
．
已知α，β是一元二次方程x2-5x-2=0的两个实数根，则α2+αβ+β2的值为（　　）
  • A. -1
  • B. 9
  • C. 23
  • D. 27
分析根据根与系数的关系α+β=-
b
a
，αβ=
c
a
，求出α+β和αβ的值，再把要求的式子进行整理，即可得出答案．
解答解：∵α，β是方程x2-5x-2=0的两个实数根，
∴α+β=5，αβ=-2，
又∵α2+αβ+β2=（α+β）2-βα，
∴α2+αβ+β2=52+2=27；
故选D．
点评此题考查了根与系数的关系，将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法，若方程两根为x1，x2，则x1+x2=-
b
a
，x1x2=
c
a
．
关于x的方程x2-ax+2a=0的两根的平方和是5，则a的值是（　　）
  • A. -1或5
  • B. 1
  • C. 5
  • D. -1
分析设方程的两根为x1，x2，根据根与系数的关系得到x1+x2=a，x1•x2=2a，由于x12+x22=5，变形得到（x1+x2）2-2x1•x2=5，则a2-4a-5=0，然后解方程，满足△≥0的a的值为所求．
解答设方程的两根为x1，x2，则x1+x2=a，x1•x2=2a，
∵x12+x22=5，
∴（x1+x2）2-2x1•x2=5，
∴a2-4a-5=0，
∴a1=5，a2=-1，
∵△=a2-8a≥0，
∴a=-1．
故选：D．
点评本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程的两根为x1，x2，则x1+x2=-
b
a
，x1•x2=
c
a
．也考查了一元二次方程的根的判别式．
两根的倒数和介绍：

1. 两根倒数和化成两根之和与两根之积；
2. 两根的比和反比的和化为两根之和与两根之积。
已知m，n是方程x2-x-1=0的两实数根，则
1
m
+
1
n
的值为（　　）
  • A. -1
  • B. -
    1
    2
  • C.
    1
    2
  • D. 1
分析先根据根与系数的关系得到m+n=1，mn=-1，再利用通分把
1
m
+
1
n
变形为
m+n
mn
，然后利用整体代入的方法计算．
解答根据题意得m+n=1，mn=-1，
所以
1
m
+
1
n
=
m+n
mn
=
1
-1
=-1．
故选：A．
点评本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程两根为x1，x2，则x1+x2=-
b
a
，x1•x2=
c
a
．
已知关于x的方程kx2-2（k+1）x+k-1=0有两个不相等的实数根．
（1）求k的取值范围；
（2）是否存在实数k，使此方程的两个实数根的倒数和等于0？若存在，求出k的值；若不存在，说明理由．
分析（1）根据方程有两个不相等的实数根可知△=[-2（k+1）]2-4k（k-1）＞0，求得k的取值范围；
（2）可假设存在实数k，使得方程的两个实数根x1，x2的倒数和为0，列出方程即可求得k的值，然后把求得的k值代入原式中看看与已知是否矛盾，如果矛盾则不存在，如果不矛盾则存在．
解答（1）∵方程有两个不相等的实数根，
∴△=[-2（k+1）]2-4k（k-1）=12k+4＞0，且k≠0，
解得k＞-
1
3
，且k≠0，
即k的取值范围是k＞-
1
3
，且k≠0；
（2）假设存在实数k，使得方程的两个实数根x1，x2的倒数和为0，
则x1，x2不为0，且
1
x1
+
1
x2
=0，
即
k-1
k
≠0，且
2(k+1)
k
k-1
k
=0，
解得k=-1，
而k=-1与方程有两个不相等实根的条件k＞-
1
3
，且k≠0矛盾，
故使方程的两个实数根的倒数和为0的实数k不存在．
点评本题主要考查了根的判别式的运用和给定一个条件判断是否存在关于字母系数的值令条件成立．解决此类问题，要先假设存在，然后根据条件列出关于字母系数的方程解出字母系数的值，再把求得的字母系数值代入原式中看看与已知是否矛盾，如果矛盾则不存在，如果不矛盾则存在．
已知m和n是方程2x2-5x-3=0的两根，则
1
m
+
1
n
=    ．
分析利用根与系数的关系可以求得m+n=-
b
a
，m•n=
c
a
代入代数式求解即可．．
解答解：∵m和n是方程2x2-5x-3=0的两根，
∴m+n=-
b
a
=-
-5
2
=
5
2
，m•n=
c
a
=-
3
2
，
∴
1
m
+
1
n
=
m+n
mn
=
5
2
-
3
2
=-
5
3

故答案为-
5
3
．
点评本题考查了根与系数的关系，解题的关键是牢记根与系数的关系并对代数式进行正确的变形．
已知关于x的方程x2+6x+k=0的两个根分别是x1、x2，且
1
x1
+
1
x2
=3，则k的值为    ．
分析首先根据一元二次方程根与系数得到两根之和和两根之积，然后把
1
x1
+
1
x2
=3转换为
x1+x2
x1x2
=3，然后利用前面的等式即可得到关于k的方程，解方程即可求出结果．
解答∵关于x的方程x2+6x+k=0的两个根分别是x1、x2，
∴x1+x2=-6，x1x2=k，
∵
1
x1
+
1
x2
=
x1+x2
x1x2
=3，
∴
-6
k
=3，
∴k=-2．
故答案为：-2．
点评此题主要考查了根与系数的关系，将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法．通过变形可以得到关于待定系数的方程解决问题．
设x1，x2是方程2x2-3x-3=0的两个实数根，则
x1
x2
+
x2
x1
的值为    ．
分析利用根与系数的关系求出两根之和与两根之积，所求式子通分并利用同分母分式的加法法则计算，变形后将各自的值代入计算即可求出值．
解答解：∵x1，x2是方程2x2-3x-3=0的两个实数根，
∴x1+x2=
3
2
，x1x2=-
3
2
，
则原式=
x12+x22
x1x2
=
(x1+x2)2-2x1x2
x1x2
=
9
4
+3
-
3
2
=
9+12
-6
=-
7
2
．
故答案为：-
7
2
点评此题考查了根与系数的关系，熟练掌握根与系数的关系是解本题的关键．
设x1、x2是方程x2+3x-3=0的两个实数根，则
x2
x1
+
x1
x2
的值为（　　）
  • A. 5
  • B. -5
  • C. 1
  • D. -1
分析先利用根与系数的关系求出两根之和与两根之积，所求式子通分并利用同分母分式的加法法则计算，再利用完全平方公式变形，将两根之和与两根之积代入计算即可求出值．
解答解：∵x1、x2是方程x2+3x-3=0的两个实数根，
∴x1+x2=-3，x1x2=-3，
则原式=
(x1+x2)2-2x1x2
x1x2
=
9+6
-3
=-5．
故选B
点评此题考查了一元二次方程根与系数的关系，熟练掌握根与系数的关系是解本题的关键．
两根之差的绝对值介绍：

1. 两根之差的绝对值等于判别式开根号除以a的绝对值。
已知关于x的一元二次方程x2+(m+3)x+m+1=0．
(1)求证：无论m取何值，原方程总有两个不相等的实数根；
(2)若x1、x2是原方程的两根，且|x1-x2|=2
√2
，求m的值，并求出此时方程的两根．
分析(1)根据关于x的一元二次方程x2+(m+3)x+m+1=0的根的判别式△=b2-4ac的符号来判定该方程的根的情况；
(2)根据根与系数的关系求得x1+x2=-(m+3)，x1•x2=m+1；然后由已知条件“|x1-x2|=2
√2
”可以求得(x1-x2)2=(x1+x2)2-4x1x2=8，从而列出关于m的方程，通过解该方程即可求得m的值；最后将m值代入原方程并解方程．
解答(1)证明：∵Δ=(m+3)2-4(m+1)
=(m+1)2+4
∵无论m取何值，(m+1)2+4恒大于0
∴原方程总有两个不相等的实数根

(2)∵x1，x2是原方程的两根
∴x1+x2=-(m+3)，x1•x2=m+1
∵|x1-x2|=2
√2
∴(x1-x2)2=(2
√2
)2
∴(x1+x2)2-4x1x2=8
∴[-(m+3)]2-4(m+1)=8
∴m2+2m-3=0
解得：m1=-3，m2=1
当m=-3时，原方程化为：x2-2=0
 解得：x1=
√2
，x2=-
√2

当m=1时，原方程化为：x2+4x+2=0
 解得：x1=-2+
√2
，x2=-2-
√2
点评本题考查了根与系数的关系、根的判别式．一元二次方程ax2+bx+c=0(a≠0，a，b，c为常数)的根的判别式Δ=b2-4ac．当Δ＞0，方程有两个不相等的实数根；当Δ=0，方程有两个相等的实数根；当Δ＜0，方程没有实数根．
已知：关于x的方程kx2-（3k-1）x+2（k-1）=0
若此方程有两个实数根x1，x2，且|x1-x2|=2，则k的值为    或    （按从小到大顺序填写答案）．
分析根据根与系数的关系表示出x1+x2，x1x2，继而根据题意可得出方程，解出即可．
解答解：∵此方程有两个实数根x1，x2，
∴x1+x2=
(3k-1)
k
，x1x2=
2(k-1)
k
，
∵|x1-x2|=2，
∴（x1-x2）2=4，
∴（x1+x2）2-4x1x2=4，即
9k2-6k+1
k2
-4×
2(k-1)
k
=4，
解得：
k+1
k
=±2，
即k=1或k=-
1
3
．
点评本题考查了根的判别式及根与系数的关系，属于基础题，这些用到的知识点是需要我们熟练记忆的内容．
一元二次方程与降次介绍：

1. 掌握与一元二次方程有关的降次类问题的解题技巧。
已知a是方程x2-x-1=0的一个根，则a4-3a-2的值为    ．
分析一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．
解答解：把x=a代入方程可得，
a2-a-1=0，即a2=a+1，
∴a4-3a-2=（a2）2-3a-2
=（a+1）2-3a-2
=a2-a-1=0．
点评代数式中的字母表示的数没有明确告知，而是隐含在题设中，首先应从题设中获取等量关系a2=a+1，然后利用“整体代入法”求代数式的值．解此题的关键是降次，把a4-3a-2变形为（a2）2-3a-2，把等量关系a2=a+1代入求值．
设α，β是一元二次方程x2+3x-7=0的两个根，则α2+4α+β=    ．
分析由α，β是一元二次方程x2+3x-7=0的两个根，得出α+β=-3，α2+3α=7，再把a2+4a+β变形为a2+3α+α+β，即可求出答案．
解答解：∵α，β是一元二次方程x2+3x-7=0的两个根，
∴α+β=-3，α2+3α-7=0，
∴α2+3α=7，
∴α2+4α+β=α2+3α+α+β=7-3=4，
故答案为：4．
点评本题考查了一元二次方程根与系数的关系．解此类题目要利用解的定义找一个关于a、b的相等关系，再根据根与系数的关系求出ab的值，把所求的代数式化成已知条件的形式，代入数值计算即可．一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系为：x1+x2=-
b
a
，x1•x2=
c
a
．
已知a、β是方程x2-2x-4=0的两个实数根，则a3+8β+6的值为（　　）
  • A. -1
  • B. 2
  • C. 22
  • D. 30
分析☆根据求根公式x=
-b±
√b2-4ac
2a
求的α、β的值，然后将其代入所求，并求值．
解答解：方程x2-2x-4=0解是x=
2±
√4+16
2
，即x=1±
√5
，
∵a、β是方程x2-2x-4=0的两个实数根，
∴①当α=1+
√5
，β=1-
√5
时，
a3+8β+6，
=（1+
√5
）3+8（1-
√5
）+6，
=16+8
√5
+8-8
√5
+6，
=30；
②当α=1-
√5
，β=1+
√5
时，
a3+8β+6，
=（1-
√5
）3+8（1+
√5
）+6，
=16-8
√5
+8+8
√5
+6，
=30．
故选D．
点评本题主要考查了一元二次方程的解．解答本题时，采用了“公式法”．
m是方程x2+x-1=0的根，则式子m3+2m2+2007的值为（　　）
  • A. 2007
  • B. 2008
  • C. 2009
  • D. 2010
分析把m代入x2+x-1=0得到m2+m-1=0，即m2+m=1，把m2+m=1代入式子：m3+2m2+2007，再将式子变形为m（m2+m）+m2+2007的形式，即可求出式子的值．
解答解：∵m是方程x2+x-1=0的根，
∴m2+m-1=0，即m2+m=1，
∴m3+2m2+2007=m（m2+m）+m2+2007=m+m2+2007=1+2007=2008．
故选B．
点评代数式中的字母表示的数没有明确告知，而是隐含在题设中，首先应从题设中获取代数式m2+m的值，然后利用“整体代入法”求代数式的值．
设a，b是方程x2+x-2013=0的两个不相等的实数根，则a2+2a+b的值为    ．
分析根据方程的根的定义，把a代入方程求出a2+a的值，再利用根与系数的关系求出a+b的值，然后两者相加即可得解．
解答解：∵a，b是方程x2+x-2013=0的两个不相等的实数根，
∴a2+a-2013=0，
∴a2+a=2013，
又∵a+b=-
1
1
=-1，
∴a2+2a+b=（a2+a）+（a+b）=2013-1=2012．
故答案为：2012．
点评本题考查了根与系数的关系与一元二次方程的解的定义，考虑把a2+2a+b分成（a2+a）与（a+b）的和是解题的关键．
设x1，x2是方程x2-x-2013=0的两实数根，则x
3
1
+2014x2-2013=    ．
分析由原方程可以得到x2=x+2013，x=x2-2013；然后根据一元二次方程解的定义知，x12=x1+2013，x1=x12-2013．由根与系数的关系知x1+x2=1，所以将其代入变形后的所求代数式求值．
解答解：∵x2-x-2013=0，
∴x2=x+2013，x=x2-2013，
又∵x1，x2是方程x2-x-2013=0的两实数根，
∴x1+x2=1，
∴x
3
1
+2014x
 
2
-2013
=x1•x12+2013x2+x2-2013，
=x1•（x1+2013）+2013x2+x2-2013，
=（x1+2013）+2013x1+2013x2+x2-2013，
=x1+x2+2013（x1+x2）+2013-2013，
=1+2013，
=2014，
故答案是：2014．
点评本题考查了根与系数的关系、一元二次方程的解的定义．对所求代数式的变形是解答此题的难点．
········ THE END ········
特殊考点
下一节：
二次函数
· 二次函数
 返回乐学堂首页
题解视频
知识点视频
查看解析
查看介绍
返回例题
/
原速
1.2×
1.1×
1×
0.9×
0.8×
清屏
利用方程根的概念求值
1
若关于x的一元二次方程x2+3x+a=0有一个根是-1，则a=    ．
2
若x=-2是关于x的一元二次方程x2-
5
2
ax+a2=0的一个根，则a的值为（　　）
  • A. 1或4
  • B. -1或-4
  • C. -1或4
  • D. 1或-4
3
已知关于x的方程x2+2x+k=0的一个根是-1，则k=    ．
4
关于x的方程x2+mx-2m2=0的一个根为1，则m的值为（　　）
  • A. 1
  • B.
    1
    2
  • C. 1或
    1
    2
  • D. 1或-
    1
    2
5
一元二次方程（a+1）x2-ax+a2-1=0的一个根为0，则a=    ．
6
关于x的一元二次方程（a-1）x2+x+|a|-1=0的一个根是0，则实数a的值为（　　）
  • A. -1
  • B. 0
  • C. 1
  • D. -1或1
7
若关于x的一元二次方程ax2+bx+5=0（a≠0）的解是x=1，则2013-a-b的值是（　　）
  • A. 2018
  • B. 2008
  • C. 2014
  • D. 2012
8
已知x=1是一元二次方程x2-mx+n=0的一个根，则m2-2mn+n2的值为    ．
9
若x=1是关于x的一元二次方程x2+3mx+n=0的解，则6m+2n=    ．
10
已知x=1是方程x2+mx+n=0的一个根，则代数式m2+2mn+n2的值为（　　）
  • A. -1
  • B. 1
  • C. -2
  • D. 2
11
已知一个根求另一个根
12
关于x的一元二次方程（m+1）x2-2mx=3的一个根是3，则另一个根等于    ．
13
已知一元二次方程x2-6x+C=0有一个根为2，则另一根为（　　）
  • A. 2
  • B. 3
  • C. 4
  • D. 8
14
已知方程x2-4x+m=0的一个根为-2，则m=    ，另一个根为    ．
15
已知x=-2是方程x2+mx-6=0的一个根，则方程的另一个根是    ．
16
已知x1=-1是方程x2+mx-5=0的一个根，则m=    ，另一个根为    ．
17
已知根的个数求参数
18
已知关于x的一元二次方程x2+2x-a=0有两个相等的实数根，则a的值是（　　）
  • A. 4
  • B. -4
  • C. 1
  • D. -1
19
关于x的一元二次方程x2-3x+m=0有两个不相等的实数根，则实数m的取值范围为（　　）
  • A. m＞
    9
    4
  • B. m＜
    9
    4
  • C. m=
    9
    4
  • D. m＜-
    9
    4
20
一元二次方程x2-2x+m=0总有实数根，则m应满足的条件是（　　）
  • A. m＞1
  • B. m=1
  • C. m＜1
  • D. m≤1
21
已知关于x的一元二次方程x2+bx+b-1=0有两个相等的实数根，则b的值是    ．
22
关于x的一元二次方程x2-3x+b=0有两个不相等的实数根，则b的取值范围是    ．
23
若关于x的方程x2-x+a=0有实数根，则a的值可以是（　　）
  • A. 2
  • B. 1
  • C. 0.5
  • D. 0.25
24
若关于x的一元二次方程(k-1)x2+2x-2=0有不相等实数根，则k的取值范围是(　　)
  • A. k＞
    1
    2
  • B. k≥
    1
    2
  • C. k＞
    1
    2
    且k≠1
  • D. k≥
    1
    2
    且k≠1
25
关于x的一元二次方程kx2-4x-1=0有两个实根，则k的取值范围是(　　)
  • A. k≥-4
  • B. k≥4
  • C. k＞-4
  • D. k≥-4且k≠0
26
若关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根，则实数k的取值范围是（　　）
  • A. k＞-1
  • B. k＜1且k≠0
  • C. k≥-1且k≠0
  • D. k＞-1且k≠0
27
若关于x的方程ax2+2（a+2）x+a=0有实数解，那么实数a的取值范围是（　　）
  • A. a≥-1
  • B. a≤1
  • C. a＞-1
  • D. a＜1
28
证明方程恒有实根
29
试证明：不论m为何值，方程2x2+3(m-1)x+m2-4m-7=0总有两个不相等的实数根．
30
已知关于x的方程x2-2kx+（2k-1）=0，其判别式可以化成m（k+a）2+b的形式，所以方程有两个不同的实根。则a+b=    ．
31
整数根之判别式
32
当m是什么整数时，关于x的一元二次方程mx2-4x+4=0与x2-4mx+4m2-4m-5=0的解都是整数？
33
关于x的一元二次方程（k-3）x2-3x+2=0有两个不相等的实数根．若方程的两根均为整数，则正整数k=    ．
34
整数根之直接求根
35
关于x的一元二次方程mx2-（3m+2）x+2m+2=0．当m=    时，此方程的两个根都为正整数．
36
已知关于x的方程mx2-（m+2）x+2=0（m≠0）．当正整数m=    或    （从小到大依次填写）时，此方程的两个根都为整数．
37
已知两根的和与积求参数
38
已知一元二次方程的两根分别是2和-3，则这个一元二次方程是（　　）
  • A. x2-6x+8=0
  • B. x2+2x-3=0
  • C. x2-x-6=0
  • D. x2+x-6=0
39
若方程x2+（m2-1）x+m=0的两根互为相反数，则m的值为（　　）
  • A. 1或-1
  • B. 1
  • C. 0
  • D. -1
40
方程x2-（m+6）x+m2=0有两个相等的实数根，且满足x1+x2=x1x2，则m的值是（　　）
  • A. -2或3
  • B. 3
  • C. -2
  • D. -3或2
41
若关于x的一元二次方程x2+bx+c=0的两个实数根分别为x1=-2，x2=4，则b+c的值是（　　）
  • A. -10
  • B. 10
  • C. -6
  • D. -1
42
关于x的一元二次方程x2+（k2-4）x+k+1=0的两实数根互为相反数，则k的值是（　　）
  • A. 2
  • B. 0
  • C. ±2
  • D. -2
43
关于x的方程ax2-(3a+1)x+2(a+1)=0有两个不相等的实根x1、x2，且有x1-x1x2+x2=1-a，则a的值是(　　)
  • A. 1
  • B. -1
  • C. 1或-1
  • D. 2
44
关于x的一元二次方程x2+2x+k+1=0的两个实根x1，x2，满足x1+x2-x1x2＜-1，则k的取值范围在数轴上表示为（　　）
  • A.
  • B.
  • C.
  • D.
45
关于x的一元二次方程x2+2（m-1）x+m2=0的两个实数根分别为x1，x2，且x1+x2＞0，x1x2＞0，则m的取值范围是（　　）
  • A. m≤
    1
    2
  • B. m≤
    1
    2
    且m≠0
  • C. m＜1
  • D. m＜1且m≠0
46
两根平方和
47
已知m，n是关于x的一元二次方程x2-3x+a=0的两个解，若（m-1）（n-1）=-6，则a的值为（　　）
  • A. -10
  • B. 4
  • C. -4
  • D. 10
48
已知一元二次方程x2-2x-2010=0的两根分别是x1和x2，则（1-x1）（1-x2）=    ．
49
已知m、n是方程x2+2
√2
x+1=0的两根，则代数式
√m2+n2+3mn
的值为（　　）
  • A. 9
  • B. ±3
  • C. 3
  • D. 5
50
方程x2+2kx+k2-2k+1=0的两个实数根x1，x2满足x
2
1
+x
2
2
=4，则k的值为    ．
51
已知α，β是一元二次方程x2-5x-2=0的两个实数根，则α2+αβ+β2的值为（　　）
  • A. -1
  • B. 9
  • C. 23
  • D. 27
52
关于x的方程x2-ax+2a=0的两根的平方和是5，则a的值是（　　）
  • A. -1或5
  • B. 1
  • C. 5
  • D. -1
53
两根的倒数和
54
已知m，n是方程x2-x-1=0的两实数根，则
1
m
+
1
n
的值为（　　）
  • A. -1
  • B. -
    1
    2
  • C.
    1
    2
  • D. 1
55
已知关于x的方程kx2-2（k+1）x+k-1=0有两个不相等的实数根．
（1）求k的取值范围；
（2）是否存在实数k，使此方程的两个实数根的倒数和等于0？若存在，求出k的值；若不存在，说明理由．
56
已知m和n是方程2x2-5x-3=0的两根，则
1
m
+
1
n
=    ．
57
已知关于x的方程x2+6x+k=0的两个根分别是x1、x2，且
1
x1
+
1
x2
=3，则k的值为    ．
58
设x1，x2是方程2x2-3x-3=0的两个实数根，则
x1
x2
+
x2
x1
的值为    ．
59
设x1、x2是方程x2+3x-3=0的两个实数根，则
x2
x1
+
x1
x2
的值为（　　）
  • A. 5
  • B. -5
  • C. 1
  • D. -1
60
两根之差的绝对值
61
已知关于x的一元二次方程x2+(m+3)x+m+1=0．
(1)求证：无论m取何值，原方程总有两个不相等的实数根；
(2)若x1、x2是原方程的两根，且|x1-x2|=2
√2
，求m的值，并求出此时方程的两根．
62
已知：关于x的方程kx2-（3k-1）x+2（k-1）=0
若此方程有两个实数根x1，x2，且|x1-x2|=2，则k的值为    或    （按从小到大顺序填写答案）．
63
一元二次方程与降次
64
已知a是方程x2-x-1=0的一个根，则a4-3a-2的值为    ．
65
设α，β是一元二次方程x2+3x-7=0的两个根，则α2+4α+β=    ．
66
已知a、β是方程x2-2x-4=0的两个实数根，则a3+8β+6的值为（　　）
  • A. -1
  • B. 2
  • C. 22
  • D. 30
67
m是方程x2+x-1=0的根，则式子m3+2m2+2007的值为（　　）
  • A. 2007
  • B. 2008
  • C. 2009
  • D. 2010
68
设a，b是方程x2+x-2013=0的两个不相等的实数根，则a2+2a+b的值为    ．
69
设x1，x2是方程x2-x-2013=0的两实数根，则x
3
1
+2014x2-2013=    ．
70
········ THE END ········
特殊考点
下一节：
二次函数
· 二次函数
返回乐学堂首页
71