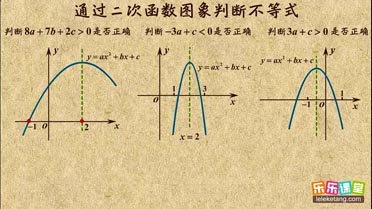
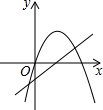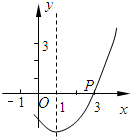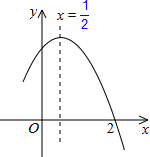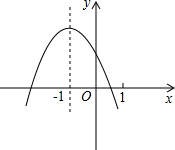看图象判断abc介绍：
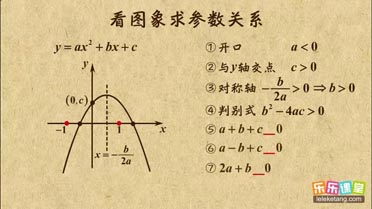
1. 二次项系数a决定抛物线的开口方向和大小；
2. 一次项系数b和二次项系数a共同决定对称轴的位置；
3. 常数项c决定抛物线与y轴交点；
4. 判别式决定抛物线与x轴交点个数。
图象分析大杂烩介绍：
1. 利用代数变形分析含参函数图象的参数关系：这类问题，一定要先写出对称轴满足的关系，以及特殊式，然后再进行消元等代数变形；
2. 看到am^2+bm，就要想到am^2+bm就加一个c，这就是x=m时的函数值。
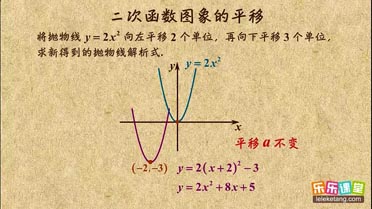
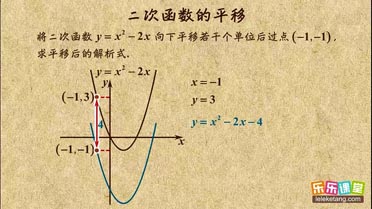
二次函数图象的平移1介绍：
1. 由于抛物线平移后的形状不变，故a不变，所以只考虑平移后的顶点坐标，即可求出解析式。
二次函数图象的平移2介绍：
1. 平移二次函数图象的关键是要搞清楚平移后的二次函数图象的顶点。
二次函数图象的变换介绍：
二次函数图象的变换只要搞清楚两点：
1. 变换后开口方向方向是否变化，不变a就不变，改变a就变成相反数；
2. 变换后顶点位置。
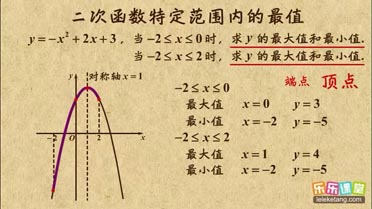
二次函数特定范围内的最值介绍：
1. 求特定范围内二次函数的最值。
二次函数最值之解析式含参介绍：
1. 讨论对称轴与x的范围的关系求最值。
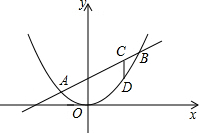
直线与抛物线的交点介绍：
1. 求直线与抛物线的交点只要联立直线方程和抛物线方程，消去y，然后解出含x的一元二次方程即可。
看图写范围介绍：
1. 利用函数的观点解形如ax^2+bx+c>kx+m的不等式：只要看图观察相应的范围就好。
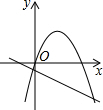
抛物线与直线的垂直距离介绍：
1. 抛物线与直线的交点与抛物线上点构成三角形的面积最值问题。
定价问题介绍：
1. 利用二次函数解决利润问题：在商品经营活动中，经常会遇到求最大利润，最大销量等问题。解此类题的关键是通过题意，确定出二次函数的解析式，然后确定其最大值。
········ THE END ········
特殊考点
下一节：
图形的旋转
返回乐学堂首页
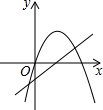
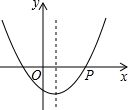
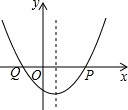解：设抛物线与x轴的另一个交点是Q，
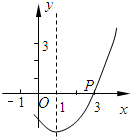
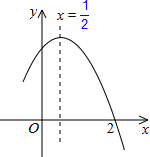
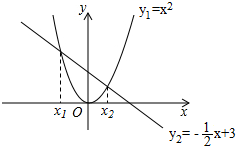解：由y1=y2，即x2=
