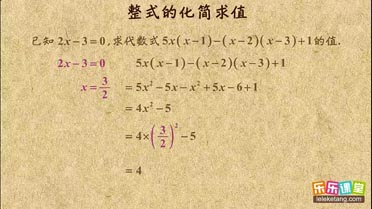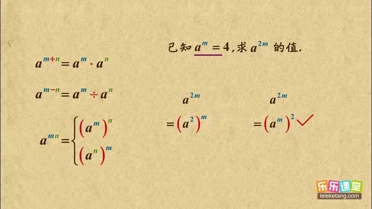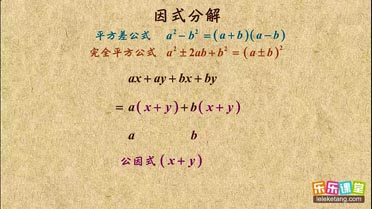整式的化简与求值介绍:
1. 整式的化简与求值:先按运算顺序把整式化简,再把对应字母的值代入求整式的值;有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似。
同底数幂的拆解与变形介绍:
1. 掌握两类同底数幂的变形技巧。
关联底数幂的变形技巧介绍:
1. 能够把以4,8,16为底的数,转化成以2或者以4为底的幂;
2. 能够把以9,27为底的数,转化成以3为底的幂。
利用积的乘方巧算介绍:
1. 理解积的乘方运算法则,能进行积的乘方运算及逆用;
2. 能够巧算底数乘积为1或﹣1的积的乘方。
整式乘法的系数问题介绍:
1. 整式化简之后的系数问题。
已知x、y的积与和求代数式的值介绍:
1. 已知x、y的积与和求与x、y有关的对称式。
分组分解法介绍:
1. 用分组分解法的概念:分组分解法一般是针对四项或四项以上多项式的因式分解,分组有两个目的,一是分组后能出现公因式,二是分组后能应用公式;
2. 对于常见的四项式,一般的分组分解有两种形式:
①二二分法;
②三一分法。
十字相乘法介绍:
1. 十字相乘法:借助画十字交叉线分解系数,从而帮助我们把二次三项式分解因式的方法,通常叫做十字相乘法;
2. x^2+(p+q)x+pq型的式子的因式分解。这类二次三项式的特点是:二次项的系数是1;常数项是两个数的积;可以直接将某些二次项的系数是1的二次三项式因式分解:x^2+(p+q)x+pq=(x+p)(x+q)。
非首一的十字相乘法介绍:
1. 二次项系数不是1的一元二次式的分解方法。
利用因式分解求值介绍:
1. 利用因式分解求代数式的值的关键就是要利用因式分解先对代数式变形,然后再求值。
利用配方求值介绍:
1. 配方法的理论依据是公式a^2±2ab+b^2=(a±b)^2;
2. 配方法的关键是:先将一元二次方程的二次项系数化为1,然后在方程两边同时加上一次项系数一半的平方。
········ THE END ········
特殊考题
下一节:
分式及其基本性质
返回乐学堂首页