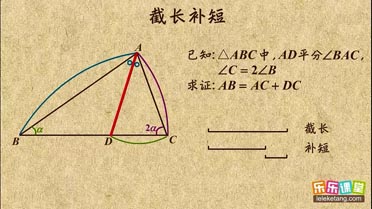
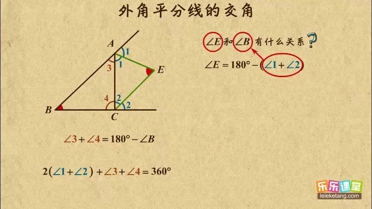
| 1 |
| 2 |
| 1 |
| 2 |

 解:∵∠A=60°,
解:∵∠A=60°,| 1 |
| 2 |

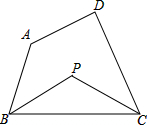
 解:∵∠BIC=100°,
解:∵∠BIC=100°,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

| 1 |
| 2 |
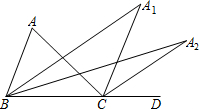
 解:∵∠ABC的平分线与∠ACB的外角平分线相交于D点,
解:∵∠ABC的平分线与∠ACB的外角平分线相交于D点,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

| m |
| 22013 |
| 3m |
| 22013 |
| m |
| 22014 |
| 3m |
| 22014 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 22013 |
| m |
| 22013 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 22013 |
| m |
| 22013 |
| m |
| 22013 |
| 1 |
| 2 |


| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| θ |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| θ |
| 22 |
| θ |
| 2n |
| θ |
| 2 |
| θ |
| 2n |
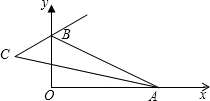
 解:∵BC是∠OBA的外角平分线,
解:∵BC是∠OBA的外角平分线,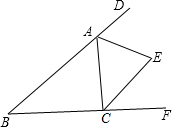
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 227° |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 227° |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 50° +180° |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
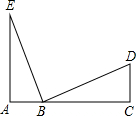

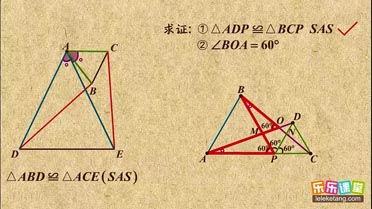
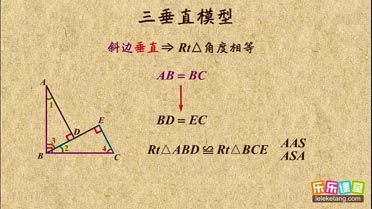
| { | ∠ABD=∠CAE ∠BDA=∠AEC AB=AC |

| { | ∠ECF=∠B EC=BC ∠ACB=∠FEC=90° |

| { | ∠AFB=∠DEA=90° ∠FBA=∠EAD AB=DA |

| { | ∠ADC=∠CEB=90° ∠BCE=∠CAD AC=BC |

| { | ∠ECF=∠B EC=BC ∠ACB=∠FEC=90° |






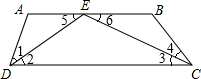 解:∵∠ADC的平分线与∠BCD的平分线的交点E恰在AB上,
解:∵∠ADC的平分线与∠BCD的平分线的交点E恰在AB上,
| { | BC=AB ∠A=∠EBC BE=AF |

| { | AB=CA ∠BAE=∠ACD AE=CD |
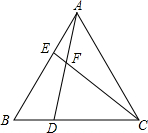
| FG |
| AF |
| 1 |
| 2 |
| 1 |
| 2 |

| { | AC=BC ∠ACE=∠BCD CE=CD |

| { | BC=AC ∠ACE=∠ CD=CE |
| { | ∠CAE=∠CBD AC=BC ∠ACB=∠ACD=60° |
| { | ∠CDB=∠CEA CE=CD ∠ACD=∠DCE=60° |





| 1 |
| 2 |
| { | AE=DE ∠EAB=∠EDC AB=DC |

| { | AB=AC ∠BAD=∠CAE AD=AE |
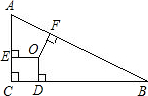


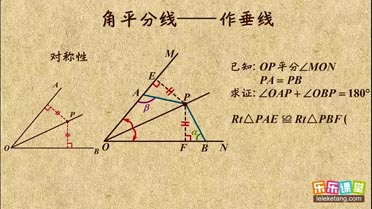
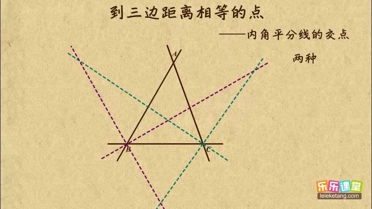
 解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,
解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,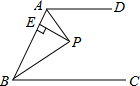
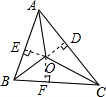
 解:过点P作MN⊥AD,
解:过点P作MN⊥AD,
 解:过点O作FG⊥AB,
解:过点O作FG⊥AB,
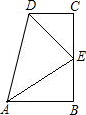
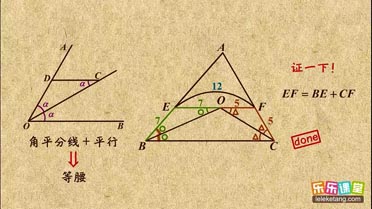
 解:如图,过点E作EF⊥AD于F,
解:如图,过点E作EF⊥AD于F,| 1 |
| 2 |

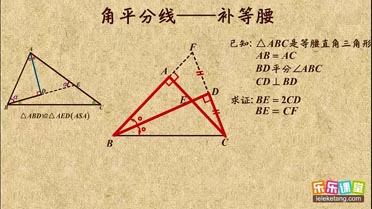
 解:如图,过点D作DH⊥AC于H,
解:如图,过点D作DH⊥AC于H,| { | DE=DG DF=DH |
 解:过点E作AD的垂线,垂足为F,
解:过点E作AD的垂线,垂足为F,
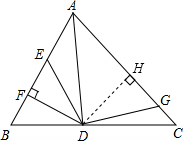 解:如图,过点D作DH⊥AC于H,
解:如图,过点D作DH⊥AC于H,| { | DE=DG DF=DH |
| 1 |
| 2 |

| { | AB=AE ∠BAD=∠EAD AD=AD |
| 1 |
| 2 |


| 1 |
| 2 |



| 1 |
| 2 |

| { | ∠BAD=∠EAD AD=AD ∠ADB=∠ADE |
| 1 |
| 2 |
| 1 |
| 2 |













| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
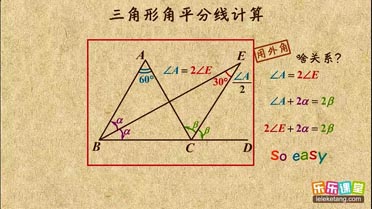


| m |
| 22013 |
| 3m |
| 22013 |
| m |
| 22014 |
| 3m |
| 22014 |

















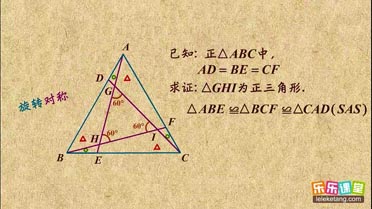



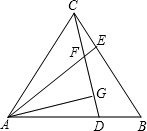
| FG |
| AF |