
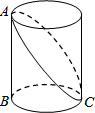
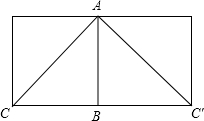
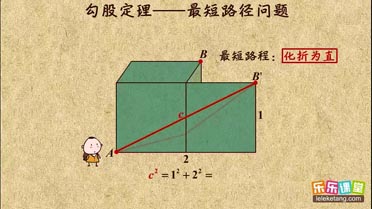
 解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
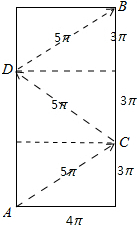 解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB;
解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB;| 2 |
| 3 |
| 6 |
| π |
| 2 |
| 3 |
| 2 |
| 3 |
 解:侧面展开图如图所示,
解:侧面展开图如图所示,| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| π |

 解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB;
解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB;| 2 |
| π |
| 2 |
| π |


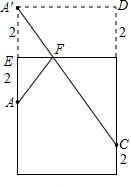 解:如图:
解:如图: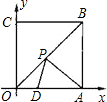
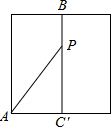
 解:连接CD,交OB于P.则CD就是PD+PA和的最小值.
解:连接CD,交OB于P.则CD就是PD+PA和的最小值.
 解:如图:
解:如图: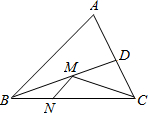
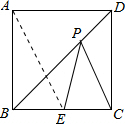
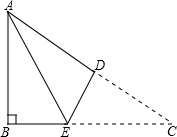
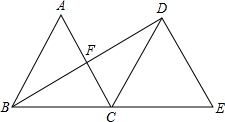
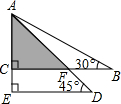
 解:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC,则CE即为CM+MN的最小值,
解:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC,则CE即为CM+MN的最小值,√2 |
| 2 |

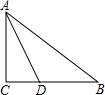
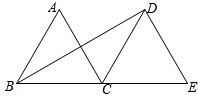
 解:在AC上取一点E,使得AE=AB,过E作EN⊥AB于N′,交AD于M,连接BM,BE,BE交AD于O,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),
解:在AC上取一点E,使得AE=AB,过E作EN⊥AB于N′,交AD于M,连接BM,BE,BE交AD于O,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),| 1 |
| 2 |




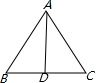
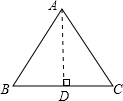
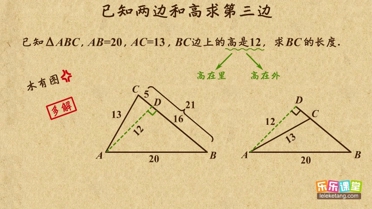
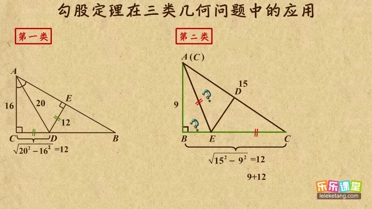
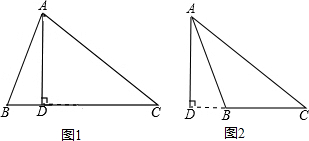 解:如图1,锐角△ABC中,AB=15,AC=20,BC边上高AD=12,
解:如图1,锐角△ABC中,AB=15,AC=20,BC边上高AD=12,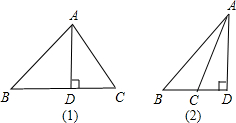

| 36 |
| 5 |
| 12 |
| 25 |
| 9 |
| 4 |
| 3 √3 |
| 4 |
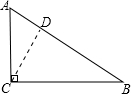
| 1 |
| 2 |
| 1 |
| 2 |
| AC•BC |
| AB |
| 9×12 |
| 15 |
| 36 |
| 5 |
| 36 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |

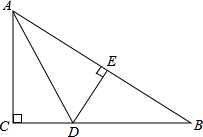
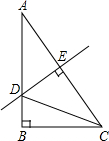
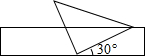
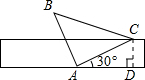
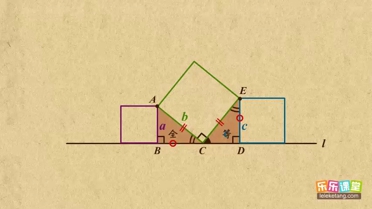
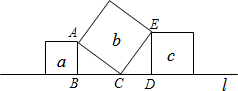 解:∵∠ACB+∠ECD=90°,∠DEC+∠ECD=90°
解:∵∠ACB+∠ECD=90°,∠DEC+∠ECD=90°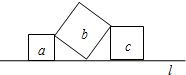
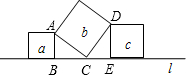 解:∵a、b、c都是正方形,
解:∵a、b、c都是正方形,| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |



√3 |
| 3 |
| 1 |
| 2 |


| 2 |
| 3 |

| 6 |
| π |
| 2 |
| π |







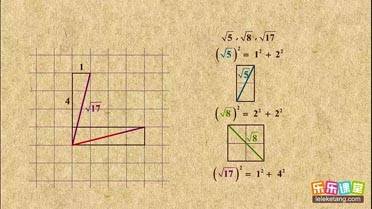








| 36 |
| 5 |
| 12 |
| 25 |
| 9 |
| 4 |
| 3 √3 |
| 4 |


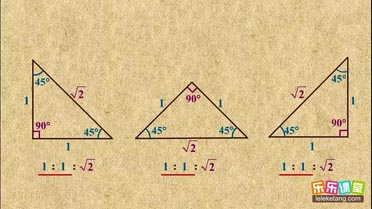






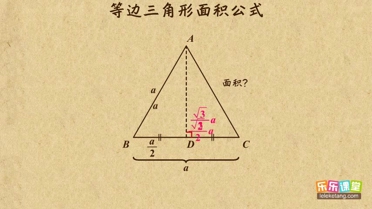
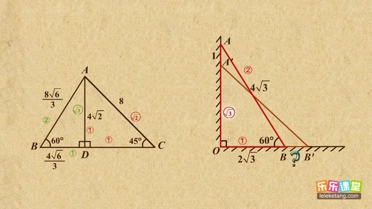



√3 |
| 3 |

