 解:如图所示:
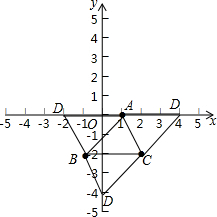
解:如图所示: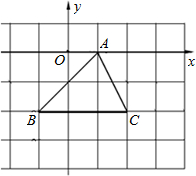 点的四边形是平行四边形,那么点D的坐标可以是( ).
点的四边形是平行四边形,那么点D的坐标可以是( ).


| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |

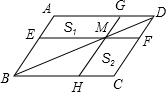
| { | AB=CD BD=DB DA=CB |

| 1 |
| 2 |

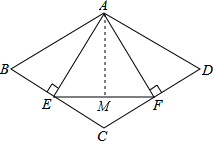
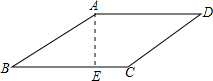 解:如图,作AE⊥BC于点E.
解:如图,作AE⊥BC于点E.| 1 |
| 2 |
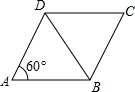
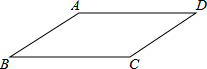 如图,在▱ABCD中,AB=4,BC=6,∠B=45°,则此平行四边形的面积是( )
如图,在▱ABCD中,AB=4,BC=6,∠B=45°,则此平行四边形的面积是( )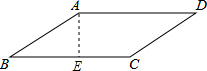 解:过点A作AE⊥BC于E,
解:过点A作AE⊥BC于E,√2 |
| 2 |
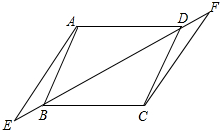
| { | AB=CD ∠ABE=∠CDF BE=DF |

| { | ∠EAO=∠FCO AO=CO ∠EOA=∠FOC |
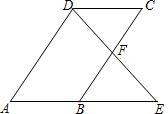
| { | ∠C=∠FBE ∠CDF=∠E CF=BF |
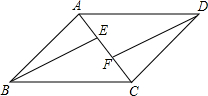
| { | AB=CD ∠BAE=∠DCF AE=CF |

| { | ∠EAO=∠FCO OA=OC ∠AOE=∠COF |
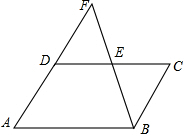
| ∥ |
| ∥ |
| ∥ |
| 1 |
| 2 |
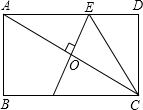
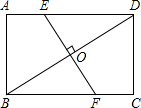
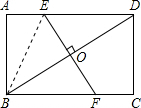 解:连接EB,
解:连接EB,| 7 |
| 8 |
| 7 |
| 8 |






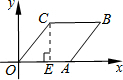 解:过C作CE⊥OA于E,
解:过C作CE⊥OA于E,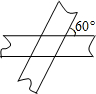
| 3 √3 |
| 2 |
| 2 √3 |
| 3 |
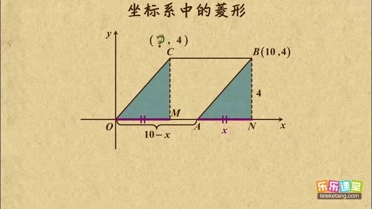
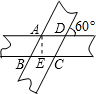 解:由题意可知:重叠部分是菱形,设菱形ABCD,则∠ABE=60°,
解:由题意可知:重叠部分是菱形,设菱形ABCD,则∠ABE=60°,√3 |
| 3 |
| 2 √3 |
| 3 |
| 2 √3 |
| 3 |
| 2 √3 |
| 3 |
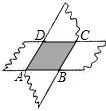
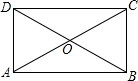
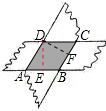 解:∵两张纸条都是长方形,
解:∵两张纸条都是长方形,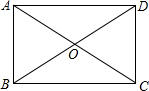
| 1 |
| 2 |
| 1 |
| 2 |


| 1 |
| 2 |
| 1 |
| 2 |
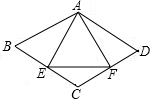
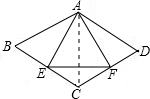
| { | AB=AD ∠B=∠D BE=DF |
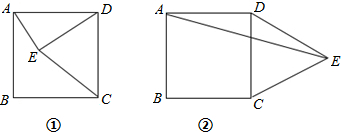
| 1 |
| 2 |
| 1 |
| 2 |
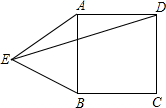


| { | ∠ABE=∠DAF AB=AD ∠BAE=∠D |
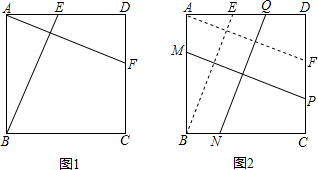
| { | ∠ABE=∠DAF AB=AD ∠BAE=∠D |
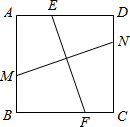
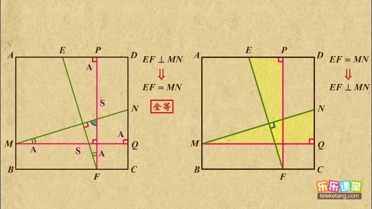
 解:①若MN=EF,则必有MN⊥EF,这句话是正确的.
解:①若MN=EF,则必有MN⊥EF,这句话是正确的. ②若MN⊥EF,则MN=EF这句话是对的;
②若MN⊥EF,则MN=EF这句话是对的;
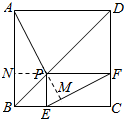
| { | NP=EP ∠ANP=∠EPF AN=PF |
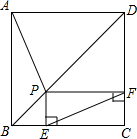
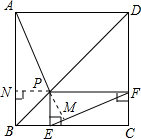
| { | AN=FP NP=EP AP=EF |
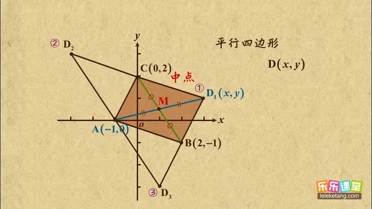
 点的四边形是平行四边形,那么点D的坐标可以是( ).
点的四边形是平行四边形,那么点D的坐标可以是( ).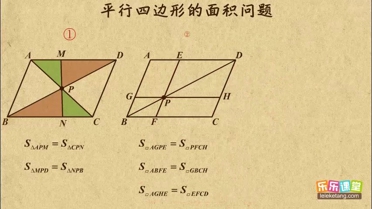



| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |



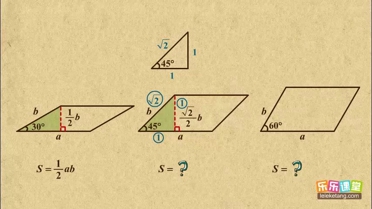
 如图,在▱ABCD中,AB=4,BC=6,∠B=45°,则此平行四边形的面积是( )
如图,在▱ABCD中,AB=4,BC=6,∠B=45°,则此平行四边形的面积是( )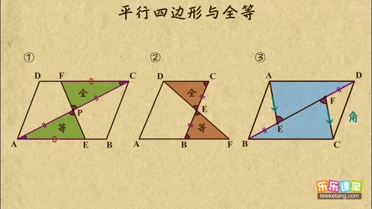









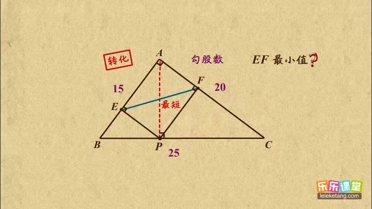






| 3 √3 |
| 2 |
| 2 √3 |
| 3 |