
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2×(-1) |
| 4×(-1)c-b2 |
| 4×(-1) |
| 4×(-1)c-4 |
| 4×(-1) |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |

| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| -2+0 |
| 2 |
| x1+x2 |
| 2 |
| (-2)+4 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| -1+3 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| x | -1 | 0 | 1 | 2 | 3 |
| y | 5 | 1 | -1 | -1 | 1 |
| 5 |
| 2 |
| 3 |
| 2 |
| 1+2 |
| 2 |
| 3 |
| 2 |
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | -5 | 7 | … |
| -3+5 |
| 2 |
| { | c=-8 4a-2b+c=0 a+b+c=-9 |
| { | a=1 b=-2 c=-8 |
| b |
| 2a |
| -1+m |
| 2 |
| -1+m |
| 2 |

| b |
| 2a |
| b |
| 2a |
 解:设抛物线与x轴的另一个交点是Q,
解:设抛物线与x轴的另一个交点是Q,
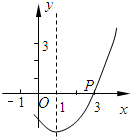

| b |
| 2a |
| b |
| 2a |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| 2a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |

| b |
| 2a |
| 1 |
| 4a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2a |
| 1 |
| 2a |
| b |
| 2a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| c |
| a |
| ||
| a |
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
| 1 |
| 2a |
| b |
| 2a |
| 1 |
| 4a |

| b |
| 2a |
| b |
| 2 |
| b |
| 2 |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 1 |
| 2 |
| { | 4a+2b-3=-3 a-b-3=0 |
| { | 4a+2b=0 a-b=3 |
| { | a=1 b=-2 |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| 5 |
| 2 |
| 3 |
| 2 |
| 49 |
| 4 |
| 3 |
| 2 |
| m-1 |
| 2 |
| m-1 |
| 2 |
| a-3 |
| 2 |
| a-3 |
| 2 |
| 7 |
| 4 |
| 7 |
| 4 |
| 7 |
| 4 |
| 4a |
| 2a |
| 1 |
| 2 |

| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
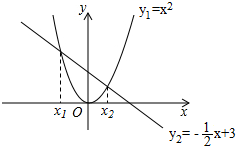 解:由y1=y2,即x2=
解:由y1=y2,即x2=| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |


| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 27 |
| 8 |
| 1 |
| 2 |
| 27 |
| 8 |
| b |
| 2a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |


| V |
| h |
| k |
| x |



| 8 |
| x |
| 10 |
| πr |
| U |
| R |
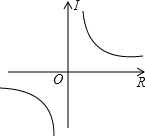
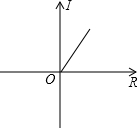
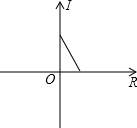

| U |
| R |
| k |
| v |

| k |
| v |
| k |
| v |
| 40 |
| v |
| 40 |
| v |
| 40 |
| v |
| 2 |
| 3 |
| 2 |
| 3 |
| 480 |
| t |
| 80 |
| t |
| t-6 |
| t |
| 480 |
| t |
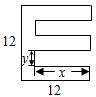

| 10 |
| x |
| 10 |
| 2x |
| 20 |
| x |
| x |
| 20 |
| 1 |
| 2 |
| 1 |
| 2 |
| 20 |
| x |
| 1 |
| 2 |
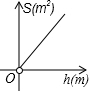
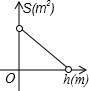
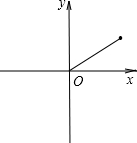
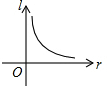
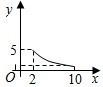
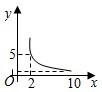
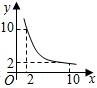
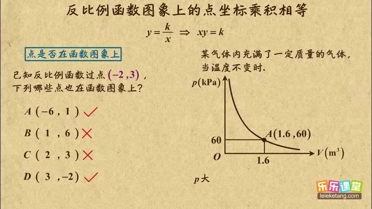
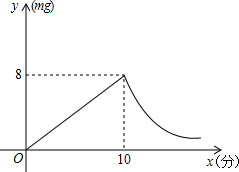 烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.当每立方米空气中含药量低于1.6mg时,对人体无毒害作用.那么从消毒开始,经 分钟学生才可以返回教室?
烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.当每立方米空气中含药量低于1.6mg时,对人体无毒害作用.那么从消毒开始,经 分钟学生才可以返回教室?| 80 |
| x |
| 4 |
| 5 |
| 4 |
| 5 |
| k2 |
| x |
| k2 |
| 10 |
| 80 |
| x |
| 80 |
| x |

| 4800 |
| x |
| k |
| x |
| k |
| 8 |
| 4800 |
| x |
| 4800 |
| x |
| 4800 |
| x |
| 8 |
| x |
| 8 |
| x-1 |
| k |
| x-1 |
| 8 |
| x-1 |
| k |
| b+3 |
| k |
| b+3 |
| k |
| 3+3 |
| 6 |
| b+3 |
| 6 |
| b+3 |
| k |
| x |
| n |
| y |
| n |
| mx |
| ||
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 2 |
| x |
| 2 |
| x |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
| k |
| x |
| k |
| x |
| 24 |
| 35 |
| 24 |
| 35 |
| 24 |
| 37 |
| 24 |
| 37 |
| 24 |
| 35 |
| k |
| V |
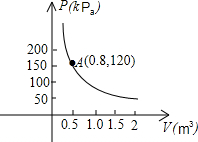
| 120×0.8 |
| V |
| 96 |
| V |
| 24 |
| 35 |
| k |
| x |
| k |
| x |

| U |
| R |
| k |
| x |
| k |
| x |
| k |
| 2 |
| k |
| x |
| k |
| 2 |
| k |
| x |
| -3 |
| x |
| -3 |
| x |
| -3 |
| x |
| k+2 |
| x |
| k+2 |
| x |
| 5 |
| x |
| 5 |
| x1 |
| 5 |
| x2 |
| 5 |
| x |
| 5 |
| x1 |
| 5 |
| x2 |
| 5 |
| x1 |
| 5 |
| x2 |
| 5(x2-x1) |
| x1x2 |
| 5(x2-x1) |
| x1x2 |
| k |
| x |
| 6 |
| x |
| 6 |
| x |
| 3+2m |
| x |
| 3 |
| 2 |
| 3 |
| 2 |
| 3+2m |
| x |
| 3+2m |
| x |
| 3+2m |
| 2 |
| 3+2m |
| 2 |
| 3 |
| 2 |
| k |
| x |

| k |
| x |
| 2 |
| x |
| k |
| x |
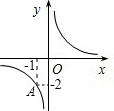
| m |
| x |

| k |
| x |
| m |
| x |

| m |
| x |
| m |
| x |
| m |
| x |
| 6 |
| x |
| 2 |
| x |

| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
| k |
| x |
| 6 |
| x |
| 4 |
| x |
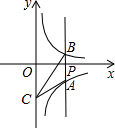
| 6 |
| x |
| 4 |
| x |
| 1 |
| 2 |
| 6 |
| x |
| 6 |
| a |
| 6 |
| a |
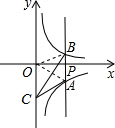
| 4 |
| x |
| 4 |
| a |
| 4 |
| a |
| 6 |
| a |
| 4 |
| a |
| 10 |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| a |
| 4 |
| x |
| 2 |
| x |

| k |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
| k |
| x |
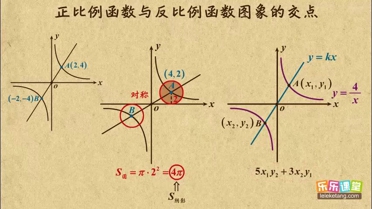
| k1 |
| x |
| k2 |
| x |

| PM |
| QM |
| k1 |
| k2 |
| 1 |
| 2 |
| 1 |
| 2 |
| PM |
| QM |
| k1 |
| k2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
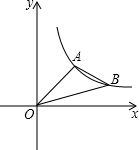
| k |
| x |
| k |
| x |
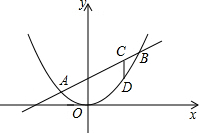
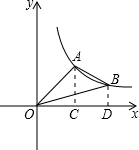 解:过A、B分别作x轴的垂线,垂足分别为C、D,如图,
解:过A、B分别作x轴的垂线,垂足分别为C、D,如图,| k |
| x |
| 4 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
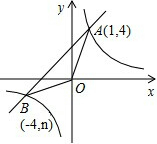
| k |
| x |
| 4 |
| x |
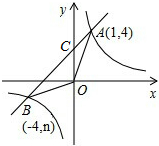 设直线y=x+3与y轴的交点为C,
设直线y=x+3与y轴的交点为C,| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
| m |
| x |

| 5 |
| 4 |
| 15 |
| 4 |
| m |
| x |
| m |
| -1 |
| 2 |
| x |
| 2 |
| x |
| 2 |
| -4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| { | -k+b=2 -4k+b=
|
| { | k=
b=
|
| 1 |
| 2 |
| 5 |
| 2 |
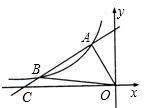
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
| 15 |
| 4 |
| k |
| x |
| m |
| x |

| m |
| x |
| m |
| x |
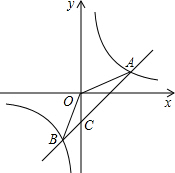
| { | 4k+b=2 -2k+b=-4 |
| { | k=1 b=-2 |
| 8 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| x |
| k |
| x |
| k |
| x |
| 1 |
| x |
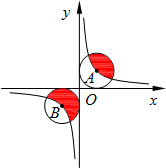
| 1 |
| x |
| k |
| x |
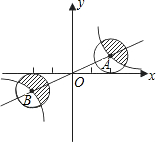
| 3 |
| x |
| 3 |
| x |
| 3 |
| x |
| 3 |
| x |
| 3 |
| x |
| 4 |
| x |

| { | y=kx① y=
|
| 4 |
| x |
| 4 |
| k |
| 4 |
| k |
| 4 |
| k |
| 4 |
| k |
| 4 |
| k |
| 4 |
| k |
| 4 |
| k |
| 4 |
| k |
| m |
| x |

| m |
| x |
| m |
| 3 |
| 6 |
| x |
| { | -1=-6k+b 2=3k+b |
| { | k=
b=1 |
| 1 |
| 3 |
| k |
| x |
| k |
| x |
| 8 |
| x |
| k |
| x |
| 8 |
| x |
| 8 |
| x |
| { | 4a+b=2 -2a+b=-4 |
| { | a=1 b=-2 |
| k2 |
| x |
| k2 |
| x |
| k |
| x |
| k |
| x |
| k |
| x |

| k |
| x |
| 2 |
| x |
| { | y=x-1 y=
|
| k |
| x |
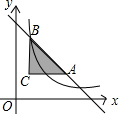
| 1 |
| x |
| 18 |
| x |
| 1 |
| x |
| 18 |
| x |
| k |
| x |
| k |
| x |
| { | y=-2x+6 y=
|
| 9 |
| 2 |
| 18 |
| x |
| 18 |
| x |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 2 |
| 3 |

| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |

| x | -1 | 0 | 1 | 2 | 3 |
| y | 5 | 1 | -1 | -1 | 1 |
| 5 |
| 2 |
| 3 |
| 2 |
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| 1 |
| 2 |
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | -5 | 7 | … |


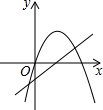







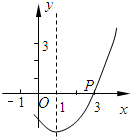

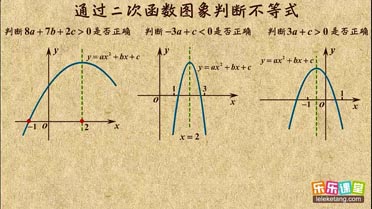
| 1 |
| 2 |
| 5 |
| 2 |
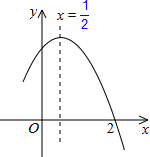


| 1 |
| 4a |

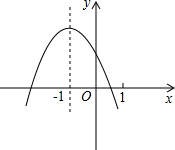
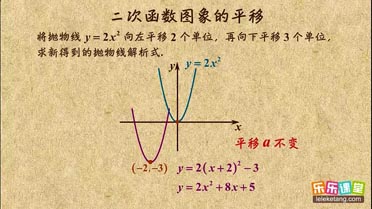
| 1 |
| 2 |
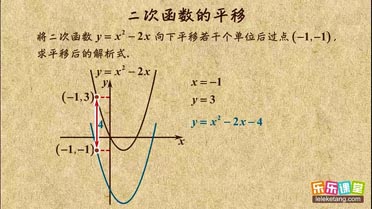
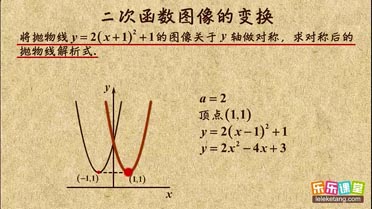
| 5 |
| 2 |
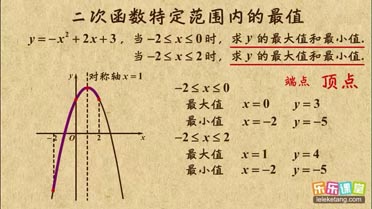
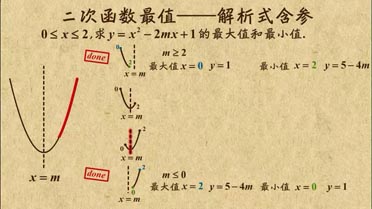
| 7 |
| 4 |
| 7 |
| 4 |
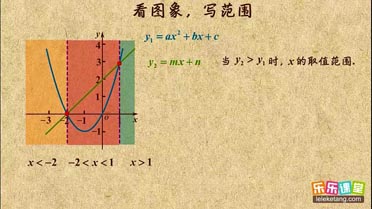
| 1 |
| 2 |

| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |





| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |













| U |
| R |




| k |
| v |

| 480 |
| t |
| 80 |
| t |
| t-6 |
| t |





| 10 |
| x |
| 10 |
| 2x |
| 20 |
| x |
| x |
| 20 |
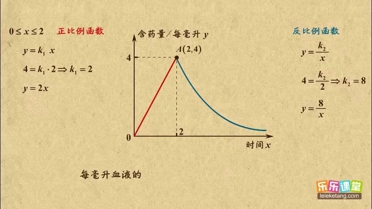
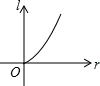
 烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.当每立方米空气中含药量低于1.6mg时,对人体无毒害作用.那么从消毒开始,经 分钟学生才可以返回教室?
烧后,y与x成反比例(如图所示).现测得药物10分钟燃烧完,此时教室内每立方米空气含药量为8mg.当每立方米空气中含药量低于1.6mg时,对人体无毒害作用.那么从消毒开始,经 分钟学生才可以返回教室?

| 8 |
| x |
| 8 |
| x-1 |
| 1 |
| x |
| 1 |
| x |

| 2 |
| x |
| 2 |
| x |

| k |
| x |

| 24 |
| 35 |
| 24 |
| 35 |
| 24 |
| 37 |
| 24 |
| 37 |
| k |
| x |

| k |
| x |
| -3 |
| x |
| k+2 |
| x |
| 5 |
| x |
| 6 |
| x |
| 3+2m |
| x |
| 3 |
| 2 |
| 3 |
| 2 |
| k |
| x |

| k |
| x |

| m |
| x |

| m |
| x |


| 6 |
| x |
| 2 |
| x |

| 6 |
| x |
| 4 |
| x |

| 4 |
| x |
| 2 |
| x |

| k1 |
| x |
| k2 |
| x |

| PM |
| QM |
| k1 |
| k2 |
| 1 |
| 2 |
| k |
| x |

| k |
| x |

| m |
| x |

| m |
| x |

| k |
| x |
| 1 |
| x |

| k |
| x |

| 3 |
| x |
| 4 |
| x |


| m |
| x |

| k |
| x |
| k2 |
| x |
| k |
| x |
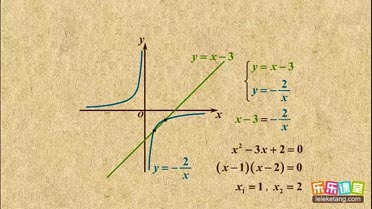
| k |
| x |

| 2 |
| x |
| k |
| x |

| 1 |
| x |
| 18 |
| x |
| 1 |
| x |
| 18 |
| x |
