| OA |
| NM |
| OB |
| BM |
| 1.52 |
| NM |
| 4 |
| 9 |

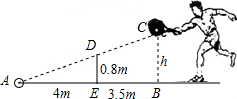 解:∵DE∥BC,
解:∵DE∥BC,| DE |
| BC |
| AE |
| AB |
| 4 |
| 4+3.5 |
| 0.8 |
| h |

| 1 |
| 2 |
| 1 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1.8 |
| 3 |
| x |
| 25 |
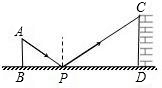
| CD |
| AB |
| PD |
| BP |
| PD |
| BP |
| 24 |
| 1.8 |
| 20 |
| 3 |
| 10 |
| 3 |
| 14 |
| 3 |
 解:如图,
解:如图,| AC |
| BD |
| CE |
| ED |
| 3 |
| 6 |
| 10-ED |
| ED |
| 20 |
| 3 |

| AB |
| AE |
| BC |
| ED |

| DE |
| BC |
| AD |
| AB |
| DE |
| BC |
| AD |
| AB |
| 3 |
| 6 |
| AD |
| 10 |
| 3×10 |
| 6 |

| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| AD |
| AE |
| AC |
| AD |
| AD |
| AE |
| AC |
| AD |

| AB |
| AC |
| AD |
| AB |
| AB2 |
| AD |
| 36 |
| 4 |






| AE |
| RF |
| BC |
| PQ |
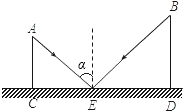
 解:∵要使△ABC∽△RPQ,
解:∵要使△ABC∽△RPQ,| AE |
| RF |
| BC |
| PQ |
| 3 |
| RF |
| 2 |
| 4 |






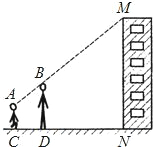
 解:过A作CN的平行线交BD于E,交MN于F.
解:过A作CN的平行线交BD于E,交MN于F.| BE |
| MF |
| AE |
| AF |
| 1.6-0.8 |
| MF |
| 1.25 |
| 1.25+30 |
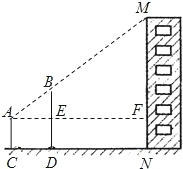
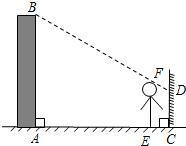 知小明的身高EF是1.7m,则楼高AB为 m(结果精确到0.1m).
知小明的身高EF是1.7m,则楼高AB为 m(结果精确到0.1m). 解:过点D作DG⊥AB,分别交AB、EF于点G、H,
解:过点D作DG⊥AB,分别交AB、EF于点G、H,| FH |
| BG |
| DH |
| DG |
| 0.5 |
| BG |
| 0.8 |
| 30 |

| AB |
| AD |
| AC |
| AE |
| AB |
| AC |
| AD |
| AE |
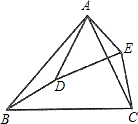
| AB |
| AD |
| AC |
| AE |
| 4 |
| 3 |

| 4 |
| 3 |
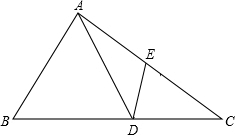
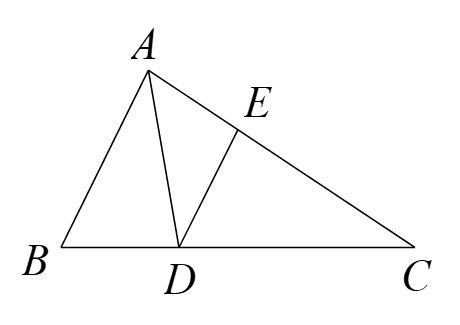
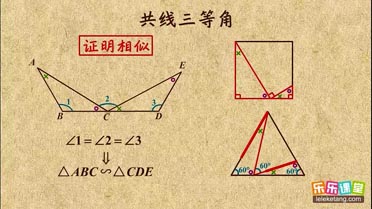
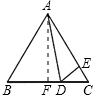 解:∵△ABC是等边三角形,∠ADE=60°,
解:∵△ABC是等边三角形,∠ADE=60°,| AB |
| DC |
| BD |
| CE |
| 4 |
| 3 |
| x |
| x-4 |
| 4 | ||
|
√3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

| AB |
| CD |
| BD |
| CE |
| AB |
| AB-3 |
| 3 |
| 2 |

| BE |
| EF |
| AB |
| DE |
| BE |
| EF |
| AB |
| DE |
| 10 |
| EF |
| 6 |
| 4 |
| 20 |
| 3 |
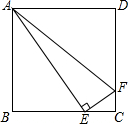
| x(4-x) |
| 4 |
| x(4-x) |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| AB |
| EC |
| BE |
| FC |
| 4 |
| 4-x |
| x |
| FC |
| x(4-x) |
| 4 |
| x(4-x) |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |

| AE |
| CD |
| AB |
| DE |
| x |
| 2 √3 |
| 2 √3 |
| 8-x |

| AD |
| BP |
| AP |
| BE |
| 10 |
| 10-x |
| x |
| y |
| 1 |
| 10 |
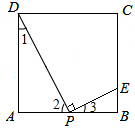 解:设AP=x,BE=y.
解:设AP=x,BE=y.| AD |
| BP |
| AP |
| BE |
| 10 |
| 10-x |
| x |
| y |
| 1 |
| 10 |
| 1 |
| 10 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
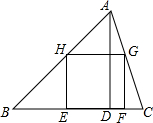
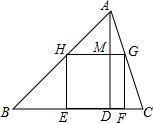 解:设AD与HG的交点为M,
解:设AD与HG的交点为M,| HG |
| BC |
| AM |
| AD |
| HG |
| 21 |
| 15-HG |
| 15 |
| 35 |
| 4 |
| 35 |
| 4 |

| 4-λ |
| 4 |
| λ |
| 6 |
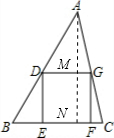 解:如图,过点A作AN⊥BC,交DG于点M;
解:如图,过点A作AN⊥BC,交DG于点M;| 1 |
| 2 |
| 4-λ |
| 4 |
| λ |
| 6 |
| 12 |
| 5 |
| 12 |
| 5 |

| 1 |
| 6 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
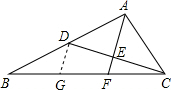 解:过点D作DG∥AF交CB于点G,
解:过点D作DG∥AF交CB于点G,| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| AB |
| AD |
| 2 |
| 3 |
| AE |
| AC |

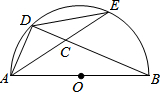
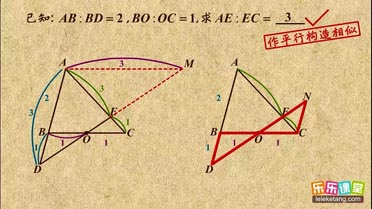
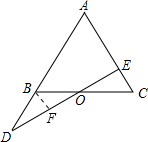 ∵BF∥AC,
∵BF∥AC,| { | ∠FBO=∠C ∠BFO=∠CEO BO=CO |
| AB |
| AD |
| 2 |
| 3 |
| BD |
| AD |
| 1 |
| 3 |
| BD |
| AD |
| BF |
| AE |
| 1 |
| 3 |
| CE |
| AE |
| 1 |
| 3 |
| AE |
| AC |
| AE |
| CE+AE |
| 3 |
| 4 |
| 3 |
| 4 |

| AB |
| AC |
| BD |
| CD |
| BD |
| CD |
| 3 |
| 4 |
| 3 |
| 7 |
| 30 |
| 7 |
| AE |
| EC |
| 2 |
| 3 |
| AB |
| AC |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 3 |
| 5 |
| AB |
| AC |
| AE |
| EC |
| 2 |
| 3 |
| AB |
| AC |
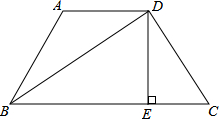
| CD |
| BD |
| DE |
| BE |
| CD |
| 5 |
| 3 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
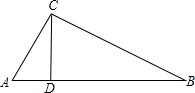
| AC |
| CD |
| BC |
| AB |
| BC |
| AB |
| BD |
| BC |
| AC |
| AD |
| AB |
| AC |
| CD |
| BD |
| AD |
| CD |




| 1 |
| 2 |
| 1 |
| 2 |



| 20 |
| 3 |
| 10 |
| 3 |
| 14 |
| 3 |



| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |

















 知小明的身高EF是1.7m,则楼高AB为 m(结果精确到0.1m).
知小明的身高EF是1.7m,则楼高AB为 m(结果精确到0.1m).


| 4 |
| 3 |









| 1 |
| 6 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 3 |
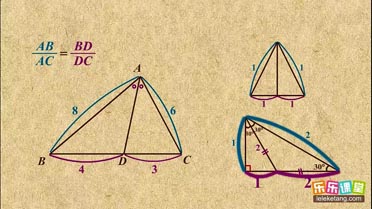
| AB |
| AD |
| 2 |
| 3 |
| AE |
| AC |


| AE |
| EC |
| 2 |
| 3 |
| AB |
| AC |

| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 3 |
| 5 |