
| 1 |
| 3 |
| 1 |
| 3 |

| 2sin30° |
| 2cos30°-1 |
| sin60°-tan45° |
| tan60°-2tan45° |
| 1 |
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
| 4 |
| 3 |
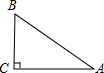
| 3 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
√2 |
| 2 |
√3 |
| 2 |
| 1 |
| 2 |

| 1 |
| 2 |
| 5 |
| 13 |
| 12 |
| 13 |
| 5 |
| 12 |
| 13 |
| 12 |
| 12 |
| 5 |
| 5 |
| 13 |

| 5 |
| 13 |
| AC |
| BC |
| 12 |
| 5 |
| 3 |
| 5 |
| 4 |
| 3 |
| 4 |
| 5 |
| 5 |
| 4 |
| 3 |
| 4 |
| a |
| c |
| b |
| a |
| 3 |
| 5 |
| b |
| a |
| 4x |
| 3x |
| 4 |
| 3 |
| 3 |
| 5 |
| 4 |
| 5 |
| sinB |
| cosB |
| ||
|
| 4 |
| 3 |

| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
√2 |
| 4 |
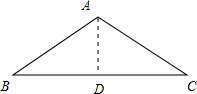
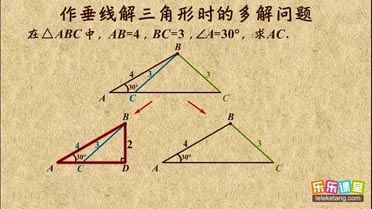
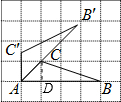 解:过C点作CD⊥AB,垂足为D.
解:过C点作CD⊥AB,垂足为D.| CD |
| BD |
| 1 |
| 3 |
| 1 |
| 3 |

| 1 |
| 2 |
√5 |
| 5 |
√10 |
| 10 |
| 2 √5 |
| 5 |
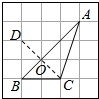 解:如图:在B点正上方找一点D,使BD=BC,连接CD交AB于O,
解:如图:在B点正上方找一点D,使BD=BC,连接CD交AB于O,| OC |
| AC |
√2 |
√10 |
√5 |
| 5 |

| 1 |
| 3 |
| 1 |
| 2 |
√2 |
| 2 |
| 2 |
| 6 |
| 1 |
| 3 |

| 1 |
| 2 |
√2 |
| 2 |
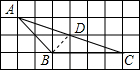 解:连接BD,则△ABD是直角三角形,∠ABD=90°,
解:连接BD,则△ABD是直角三角形,∠ABD=90°,| BD |
| AB |
√2 |
| 2 √2 |
| 1 |
| 2 |
| 4 |
| 5 |

| 4 |
| 5 |
| 3 |
| 5 |
| sinB |
| cosB |
| 3 |
| 4 |
| AD |
| sinB |
| 4 | ||
|
| 20 |
| 3 |
| AC |
| AB |
| 3 |
| 4 |
| 20 |
| 3 |
| 1 |
| 3 |

| AD |
| AB |
| 1 |
| 3 |

| CE |
| tan26° |

| CE |
| tan26° |
| 15 |
| 0.49 |

| BC |
| tan30° |
| 5 | ||
|
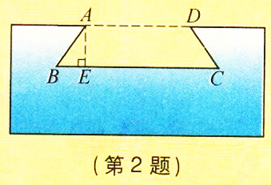
 m,求屋面AB的坡度和支架BF的长.
m,求屋面AB的坡度和支架BF的长.| 1 |
| 3 |
| 31 |
| 50 |
| 21 |
| 25 |
| CD |
| AD |
| OB |
| AB |
| 31 |
| 50 |

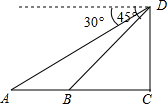
 解:作CE⊥AB于点E,
解:作CE⊥AB于点E,| BE |
| tan30° |

| OB |
| AB |
| 1 |
| 2 |
| OD |
| CD |
| 1 |
| 2 |

| AB1 |
| D1B1 |
| AB1 |
| D1C1+C1B1 |
√3 |
| 3 |
| x |
| 50+x |
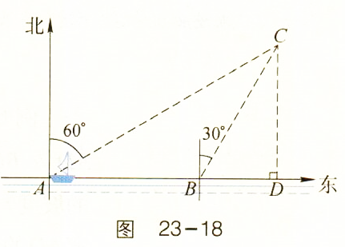
| CD |
| tan∠CAD |
| x |
| tan30° |
| CD |
| tan∠CBD |
| x |
| tan60° |
| x |
| tan30° |
| x |
| tan60° |
| x | ||
|
| x |
√3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 9 |
| 11 |
| 7 |
| 11 |

| AD |
| AC |
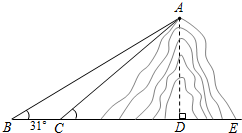
| AD |
| BD |
| AD |
| tan31° |
| x | ||
|
| 5 |
| 3 |
| AD |
| CD |
| AD |
| tan39° |
| x | ||
|
| 11 |
| 9 |
| 5 |
| 3 |
| 11 |
| 9 |
| AD |
| AC |
| AD |
| sin39° |
| 180 | ||
|
| 3 |
| 5 |
| 3 |
| 4 |
| 12 |
| 13 |
| 12 |
| 5 |
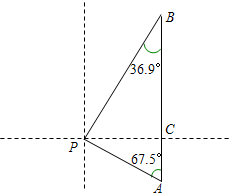
| PC |
| AC |
| PC |
| tan67.5° |
| 5x |
| 12 |
| PC |
| BC |
| x |
| tan36.9° |
| 4x |
| 3 |
| 5x |
| 12 |
| 4x |
| 3 |
| PC |
| PB |
| PC |
| sin∠B |
| 60 |
| sin36.9° |
| 5 |
| 3 |
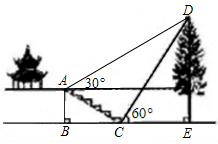
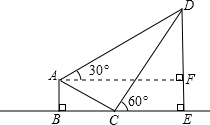 解:如图,过点A作AF⊥DE于F,
解:如图,过点A作AF⊥DE于F,| DE |
| tan60° |
√3 |
| 3 |
| AB |
| BC |
| 1 |
√3 |
| x-3 |
| tan30° |
√3 |
| 3 |

| 100 |
√3 +1 |
| 100 |
√3 -1 |
| AB |
| BC |
√3 |
| 3 |
| 100 |
√3 -1 |

| MF |
| FC |
√3 |
| 3 |
| x+0.2 |
| 28-x |
 解:过点A作AE⊥MN于E,过点C作CF⊥MN于F,
解:过点A作AE⊥MN于E,过点C作CF⊥MN于F,√3 |
| 3 |
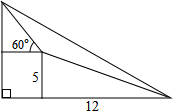
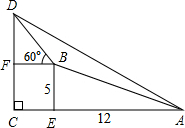 解:∵BE:AE=5:12,
解:∵BE:AE=5:12,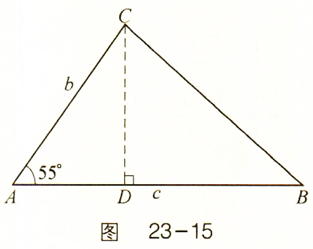
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
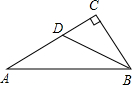
| 3 |
| 5 |
√10 |
| 5 |
| 3 |
| 10 |
| 3 √10 |
| 10 |
| BC |
| AC |
| CD |
| BC |
| DE |
| AE |
| 1 |
| 2 |
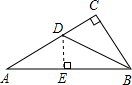 解:作DE⊥AB于点E.
解:作DE⊥AB于点E.| BC |
| AC |
| CD |
| BC |
| DE |
| AE |
| 1 |
| 2 |
| 3 √5 |
| 5 |
| 3 √5 |
| 5 |
| 6 √5 |
| 5 |
| 6 √5 |
| 5 |
| 4 √5 |
| 5 |
| DE |
| BE |
| 3 |
| 4 |
| 3 |
| 5 |
| 2 |
| 3 |

 解:如图,过点C作CD⊥AB于点D.
解:如图,过点C作CD⊥AB于点D.| 2 |
| 3 |
| CD |
| AC |
| CD |
| 6 |
| 2 |
| 3 |
| CD |
| BD |
| 4 |
| 3 |
| 4 |
| 3 |
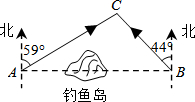
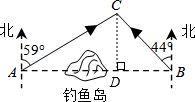 解:如图,作CD⊥AB于点D,
解:如图,作CD⊥AB于点D,| CD |
| AC |
| CD |
| cos∠ACD |
| a |
| 0.52 |
| CD |
| BC |
| CD |
| cos∠BCD |
| a |
| 0.72 |
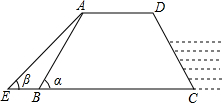
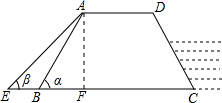
| AF |
| sin45° |
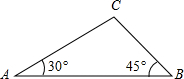

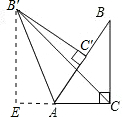 解:如图,作B′E⊥AC交CA的延长线于E.
解:如图,作B′E⊥AC交CA的延长线于E.| 1 |
| 2 |
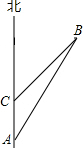
 解:作BD⊥AC于点D.
解:作BD⊥AC于点D.| x |
| AD |
| x |
| CD |
| 1 |
| 2 |
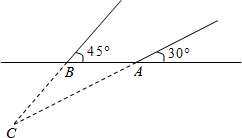
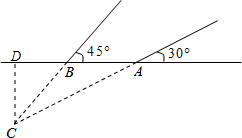 设CD=x,
设CD=x,| 4 |
√3 -1 |
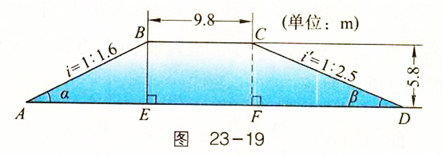
| BE |
| AE |
| 1 |
| 1.6 |
| CF |
| DF |
| 1 |
| 2.5 |
| 1 |
| 1.6 |
| 1 |
| 2.5 |
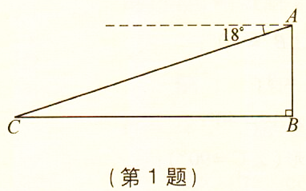


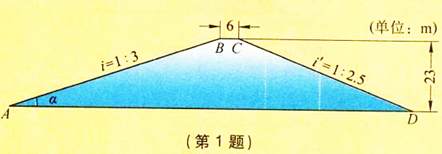

| BE |
| AE |
| 1 |
| 2.5 |
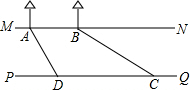
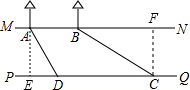 解:作AE⊥PQ于E,CF⊥MN于F.(1分)
解:作AE⊥PQ于E,CF⊥MN于F.(1分)| AE |
| tan60° |
| x |
√3 |
√3 |
| 3 |
| CF |
| tan30° |
| x | ||
|
√3 |
| 3 |


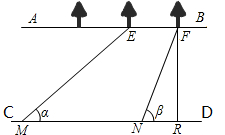
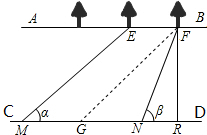 解:过点F作FG∥EM交CD于G,则MG=EF=10米.
解:过点F作FG∥EM交CD于G,则MG=EF=10米.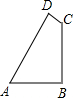
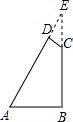 延长AD,BC交于点E.
延长AD,BC交于点E.| DE |
| cos30° |
| 3 | ||
|
| 1 |
| 2 |
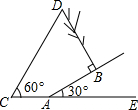
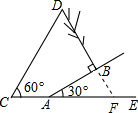 解:延长DB交AE于F,由题可得BD⊥AB,在Rt△ABF中∠BAF=30°,AB=6,
解:延长DB交AE于F,由题可得BD⊥AB,在Rt△ABF中∠BAF=30°,AB=6,| AB |
| AF |
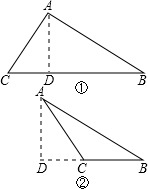 解:如图,过A作AD⊥BC(或BC的延长线)于D点.
解:如图,过A作AD⊥BC(或BC的延长线)于D点.√3 |
| 2 |

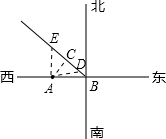 解:假设D、E为刚好受影响的点,
解:假设D、E为刚好受影响的点,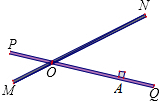
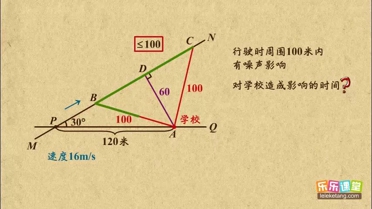
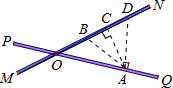 解:如图:过点A作AC⊥ON,AB=AD=200米,
解:如图:过点A作AC⊥ON,AB=AD=200米,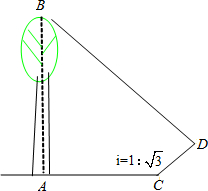
√3 |
| 3 |
| 1 |
| 2 |
| BE |
| 1 |
| DE |
| 0.8 |
| 8.8+1.6 √3 |
| 0.8 |
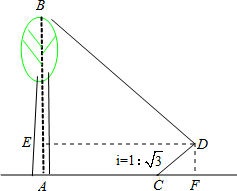 解:过点D作DE⊥AB,DF⊥AC,垂足分别为E,F,如图,
解:过点D作DE⊥AB,DF⊥AC,垂足分别为E,F,如图,√3 |
| 3 |
| 1 |
| 2 |
| BE |
| 1 |
| DE |
| 0.8 |
| 8.8+1.6 √3 |
| 0.8 |
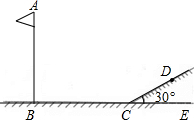
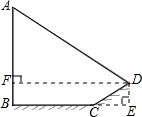
| AF |
| 20+4 √3 |
| 1.65 |
| 3.3 |
| 9 |
| 10 |
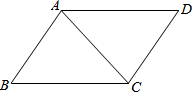
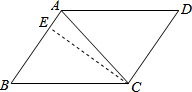 解:作CE⊥AB于点E.
解:作CE⊥AB于点E.| CE |
| BC |
| 9 |
| 10 |
 ,
,| 1 |
| 2 |
| AD |
| AB |
| 3 |
| 5 |
| 3 |
| 5 |
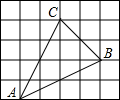
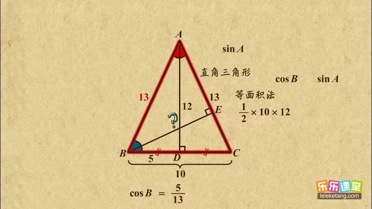
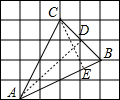 解:如图,作AD⊥BC于D,CE⊥AB于E,
解:如图,作AD⊥BC于D,CE⊥AB于E,| 1 |
| 2 |
| 1 |
| 2 |
| 2 √2 ×3√2 |
| 2 √5 |
| 6 √5 |
| 5 |
| CE |
| AC |
| ||
| 2 √5 |
| 3 |
| 5 |
| 3 |
| 5 |
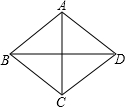
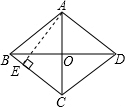 解:如图,设AC、BD相交于点O,
解:如图,设AC、BD相交于点O,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 24 |
| 5 |
| AE |
| AB |
| 24 |
| 25 |
| 24 |
| 25 |
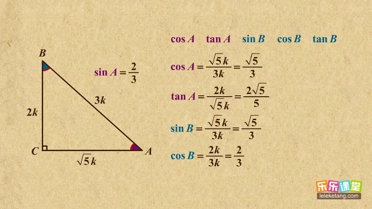
| 1 |
| 3 |

| 2sin30° |
| 2cos30°-1 |
| sin60°-tan45° |
| tan60°-2tan45° |
| 1 |
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
√2 |
| 2 |
√3 |
| 2 |
| 5 |
| 13 |
| 12 |
| 13 |
| 5 |
| 12 |
| 13 |
| 12 |
| 12 |
| 5 |
| 3 |
| 5 |
| 4 |
| 3 |
| 4 |
| 5 |
| 5 |
| 4 |
| 3 |
| 4 |
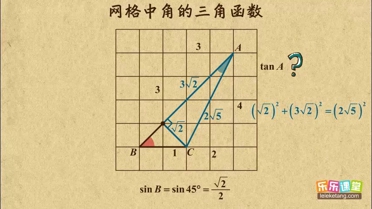

| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
√2 |
| 4 |

| 1 |
| 2 |
√5 |
| 5 |
√10 |
| 10 |
| 2 √5 |
| 5 |

| 1 |
| 3 |
| 1 |
| 2 |
√2 |
| 2 |

| 1 |
| 2 |
√2 |
| 2 |
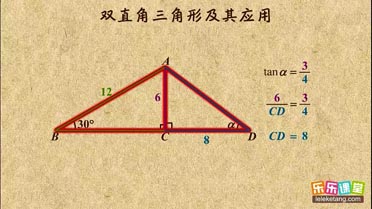
| 4 |
| 5 |

| 1 |
| 3 |



 m,求屋面AB的坡度和支架BF的长.
m,求屋面AB的坡度和支架BF的长.| 1 |
| 3 |
| 31 |
| 50 |
| 21 |
| 25 |



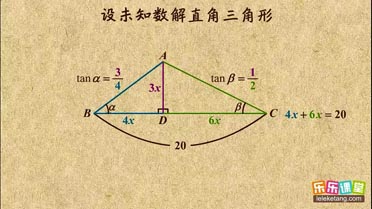


| 3 |
| 5 |
| 1 |
| 2 |
| 9 |
| 11 |
| 7 |
| 11 |

| 3 |
| 5 |
| 3 |
| 4 |
| 12 |
| 13 |
| 12 |
| 5 |



| 100 |
√3 +1 |
| 100 |
√3 -1 |


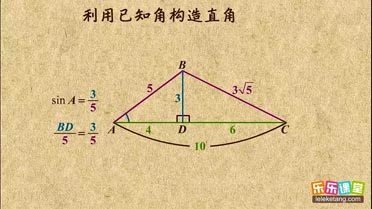
| 1 |
| 2 |

| 3 |
| 5 |
√10 |
| 5 |
| 3 |
| 10 |
| 3 √10 |
| 10 |
| 2 |
| 3 |







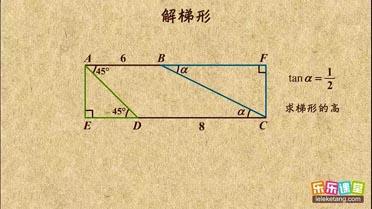










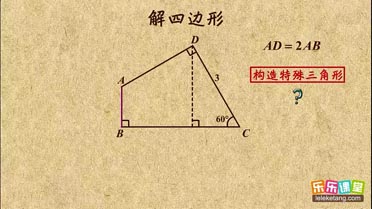






| 9 |
| 10 |



