下载高清试卷
【2021-2022学年山西省运城市盐湖区九年级(上)期末数学试卷】-第2页
试卷格式:2021-2022学年山西省运城市盐湖区九年级(上)期末数学试卷.PDF
试卷热词:最新试卷、2021年、山西试卷、运城市试卷、数学试卷、九年级上学期试卷、期末试卷、初中试卷
扫码查看解析
试卷题目
1.tan30°的相反数是( )
- A. -√3
- B. -√3
2 - C. -√3
3 - D. -√2
2
2.若二次函数y=ax2+bx-2的图象经过点(-2,0),则代数式2a-b的值为( )
- A. 0
- B. 1
- C. -1
- D. 2
3.如图所示的物体的左视图是( )


- A.
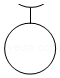
- B.
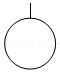
- C.
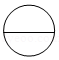
- D.

4.若将抛物线y=2x2+1先向右平移1个单位长度,再向下平移3个单位长度,则所得抛物线的表达式为( )
- A. y=2(x-1)2-2
- B. y=2(x+1)2-2
- C. y=2(x-1)2+3
- D. y=2(x+1)2+3
5.某地新高考有一项“6选3”选课制,高中学生李鑫和张锋都已选了地理和生物,现在他们还需要从“物理、化学、政治、历史”四科中选一科参加考试.若这四科被选中的机会均等,则他们恰好一人选物理,另一人选化学的概率为( )
- A.
1 8 - B.
1 4 - C.
3 8 - D.
1 2
6.对于二次函数y=-(x-1)2的图象,下列说法不正确的是( )
- A. 开口向下
- B. 对称轴是直线x=1
- C. 顶点坐标为(1,0)
- D. 当x<1时,y随x的增大而减小
7.如图,一艘轮船在小岛A的西北方向距小岛40

√2
海里的C处,沿正东方向航行一段时间后到达小岛A的北偏东60°的B处,则该船行驶的路程为( )
- A. 80海里
- B. 120海里
- C. (40+40√2)海里
- D. (40+40√3)海里
8.关于x的方程ax2+(1-a)x-1=0,下列结论正确的是( )
- A. 当a=0时,方程无实数根
- B. 当a=-1时,方程只有一个实数根
- C. 当a=1时,有两个不相等的实数根
- D. 当a≠0时,方程有两个相等的实数根
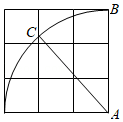
9.如图,在3×3的网格中,A,B均为格点,以点A为圆心,AB的长为半径作弧,图中的点C是该弧与格线的交点,则tan∠BAC的值是( )

- A.
1 2 - B.
2 √55 - C. √5
3 - D.
2 3
10.已知二次函数y=ax2+bx+c的图象的对称轴为直线x=1,其图象如图所示,现有下列结论:①abc>0;②2a+b=0;③4a-2b+c<0;④a+b≥m(am+b);⑤2c<3b.其中正确结论的个数是( )
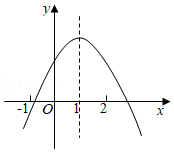
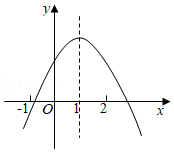
- A. 1
- B. 2
- C. 3
- D. 4
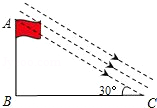
11.课外活动小组测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB在地面上的影长BC为24米,那么旗杆AB的高度约是 米.(结果保留根号)

12.已知函数y=(m-1)xm2+3是关于x的一次函数,则m的值为 .
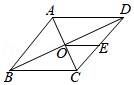
13.如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若OE=2,则菱形的周长为 .

14.抛物线y=-x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
从表可知,抛物线与x轴的另一个交点坐标为 .
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | -4 | 6 | 6 | 4 | … |
从表可知,抛物线与x轴的另一个交点坐标为 .
15.如图,正方形ABCD的边长为2,E为边AD上一动点,连接CE,以CE为边向右侧作正方形CEFG,连接DF,DG,则△DFG面积的最小值为 .


16.(1)计算:(
)-1-2tan45°+2sin60°-|1-
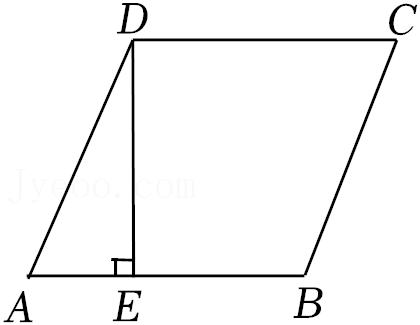
(2)如图,在菱形ABCD中,DE⊥AB于点E,BE=8,sinA=
,求菱形的边长.
| 1 |
| 2 |
√3
|.(2)如图,在菱形ABCD中,DE⊥AB于点E,BE=8,sinA=
| 12 |
| 13 |

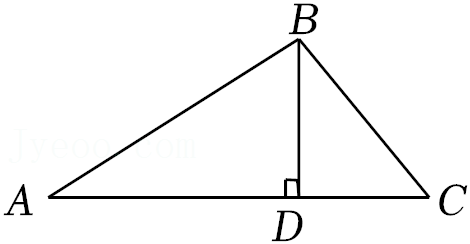
17.如图,在△ABC中,BD⊥AC,AB=4,AC=3
(1)求AD的长.
(2)求sinC的值.
√3
,∠A=30°.(1)求AD的长.
(2)求sinC的值.

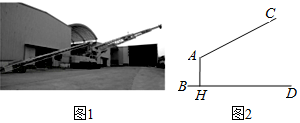
18.如图1所示的是一辆混凝土布料机的实物图,图2是其工作时部分示意图,AC是可以伸缩的布料臂,其转动点A离地面BD的高度AH为3.2米.当布料臂AC长度为8米,张角∠HAC为118°时,求布料口C离地面的高度.(结果保留一位小数;参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)

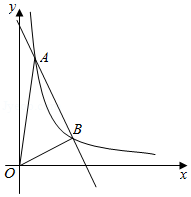
19.如图,一次函数y=kx+b与反比例函数y=
(x>0)的图象交于A(m,8),B(4,n)两点,连接OA,OB.
(1)求一次函数的表达式;
(2)求△AOB的面积.
| 8 |
| x |
(1)求一次函数的表达式;
(2)求△AOB的面积.

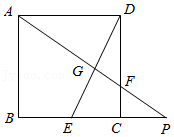
20.如图,在正方形ABCD中,E是BC的中点,点P在BC的延长线上,AP,DE交于点G,AP,CD交于点F.
(1)求证:AD•CF=CP•DF.
(2)若DF=2CF,AB=6,求DG的长.
(1)求证:AD•CF=CP•DF.
(2)若DF=2CF,AB=6,求DG的长.

21.某企业生产了一套健身器材,通过实体店和网上商店两种途径进行销售,销售一段时间后,该企业对这种健身器材的销售情况进行了为期30天的跟踪调查,其中实体店的日销售量y1(套)与时间x(x为整数,单位:天)的部分对应值如表:
(1)已知y1与x满足二次函数关系,求y1与x的函数关系式.
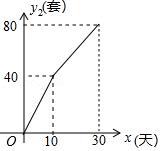
(2)网上商店的日销售量y2(套)与时间x(x为整数,单位:天)的关系如图所示,求y2与x的函数关系式并写出自变量x的取值范围.
(3)在跟踪调查的30天中,设实体店和网上商店的日销售总量为y(套),求当x为何值时,日销售总量y达到最大,并求出此时的最大值.
| 时间x(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 日销售量y1(套) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(1)已知y1与x满足二次函数关系,求y1与x的函数关系式.
(2)网上商店的日销售量y2(套)与时间x(x为整数,单位:天)的关系如图所示,求y2与x的函数关系式并写出自变量x的取值范围.
(3)在跟踪调查的30天中,设实体店和网上商店的日销售总量为y(套),求当x为何值时,日销售总量y达到最大,并求出此时的最大值.

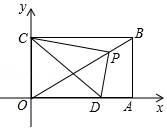
22.矩形OABC在平面直角坐标系中的位置如图所示,已知B(2
(1)当点D运动到OA的中点时,求PC2+PD2的值.
(2)在运动过程中,∠CDP的大小是否有变化?若不变,求出∠CDP的大小;若改变,请说明理由.
(3)当△ODP为等腰三角形时,直接写出点D的坐标.
√3
,2),点A在x轴上,点C在y轴上,P是对角线OB上一动点(不与原点重合),连接PC,过点P作PD⊥PC,交x轴于点D,连接CD.(1)当点D运动到OA的中点时,求PC2+PD2的值.
(2)在运动过程中,∠CDP的大小是否有变化?若不变,求出∠CDP的大小;若改变,请说明理由.
(3)当△ODP为等腰三角形时,直接写出点D的坐标.

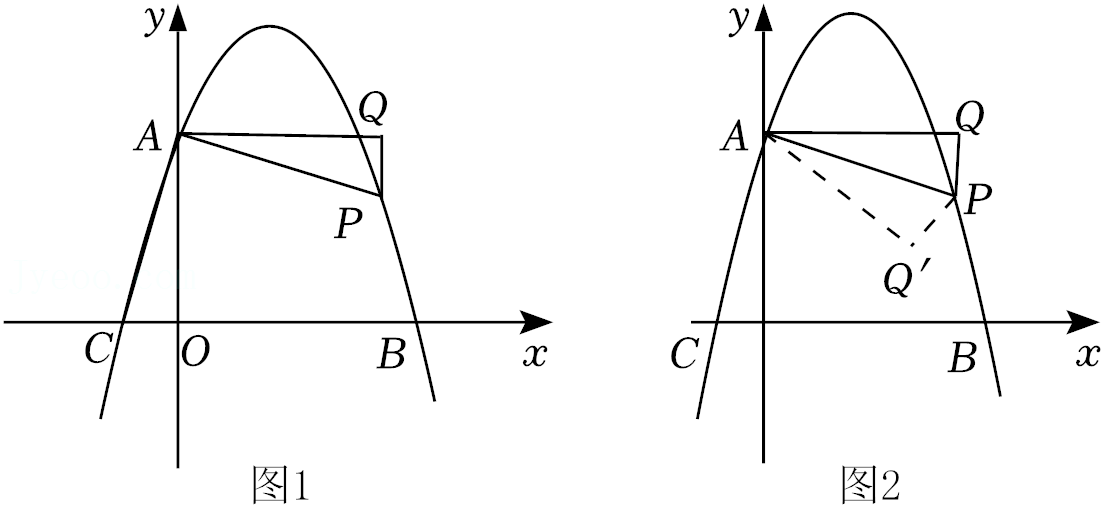
23.已知抛物线y=-x2+bx+c交x轴于B(4,0),C(-1,0)两点,交y轴于点A,P是抛物线上一动点,设点P的横坐标为m,过点P作x轴的垂线PQ,过点A作AQ⊥PQ于点Q,连接AP(AP不平行x轴).
(1)求抛物线的表达式.
(2)如图1,若△AQP∽△AOC,求点P的坐标.
(3)如图2,若点P位于抛物线的对称轴的右侧,将△APQ沿AP对折,点Q的对应点为Q',当点Q' 落在x轴上时,求点P的坐标.
(1)求抛物线的表达式.
(2)如图1,若△AQP∽△AOC,求点P的坐标.
(3)如图2,若点P位于抛物线的对称轴的右侧,将△APQ沿AP对折,点Q的对应点为Q',当点Q' 落在x轴上时,求点P的坐标.

查看全部题目
相关试卷推荐
更多热门试卷
如何查看答案以及解析
扫描右侧二维码查看试卷答案解析以及视频讲解