下载高清试卷
【2021-2022学年山西省临汾市七年级(上)期末数学试卷】-第1页
试卷格式:2021-2022学年山西省临汾市七年级(上)期末数学试卷.PDF
试卷热词:最新试卷、2022年、山西试卷、临汾市试卷、数学试卷、七年级上学期试卷、期末试卷、初中试卷

扫码查看解析
试卷题目
1.-2022的相反数是( )
- A. 2022
- B. -
1 2022 - C.
1 2022 - D. -2022
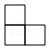
2.如图是由5个相同的小立方块搭成的几何体,则从正面看这个几何体的形状是( )
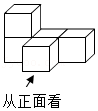

- A.
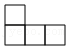
- B.
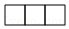
- C.
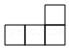
- D.
3.九曲桥是我国经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光,如图,某两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是( )


- A. 两点确定一条直线
- B. 垂线段最短
- C. 两点之间,线段最短
- D. 过一点有且只有一条直线与已知直线垂直
4.代数式5x2-x,x2y,
,x+y中是单项式的是( )
| 3 |
| x |
- A. 5x2-x
- B. x2y
- C.
3 x - D. x+y
5.山西太原有着悠久的历史,是一座名副其实的古都了,山西太原在黄河支流--汾河的孕育下,生机勃勃,经济发展前景喜人,据统计,2021年山西太原前三季度的生产总值达到了约3600亿元,数据3600亿用科学记数法可表示为( )


- A. 3.6×103
- B. 3.6×1010
- C. 3.6×1011
- D. 3.6×1012
6.下列计算正确的是( )
- A. m+n=mn
- B. m2n-nm2=0
- C. 2m3+3m2=5m5
- D. 2m3-3m2=-m
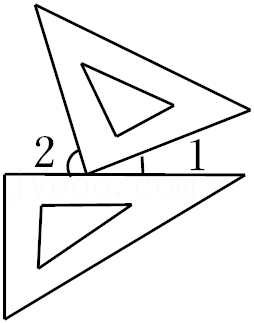
7.两直角三角板按如图所示方式摆放,若∠1=25°,则∠2等于( )

- A. 45°
- B. 55°
- C. 60°
- D. 65°
8.实数a在数轴上的对应点的位置如图所示,若实数b满足-a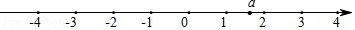
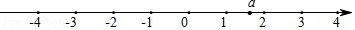
- A. 2
- B. -1
- C. -2
- D. -3
9.若x=2是关于x的一元一次方程ax-b=3的解,则4a-2b+1的值是( )
- A. 7
- B. 8
- C. -7
- D. -8
10.《孙子算经》一道问题译文如下:“用绳子去量一根木材的长,绳子还余4.5尺,将绳子对折再量木材的长,绳子比木材的长短1尺,问木材的长为多少尺?”若设木材的长为x尺,可得方程( )
- A. x-4.5=2(x+1)
- B. 2(x+4.5)=x-1
- C. 2(x-4.5)=x+1
- D. x+4.5=2(x-1)
11.请你写出一个解为x=-1的一元一次方程 .
12.2021年11月6日,山西太原降雪来袭,当天最高气温1°C,最低气温是-9°C,那么太原市这一天的温差为 °C.


13.如图,AB=4cm,BC=6cm,点D为AB的中点,则DC= cm.
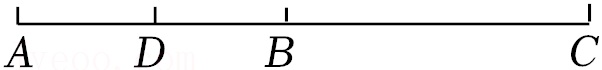
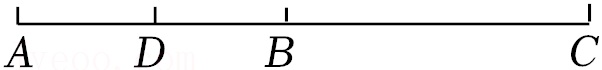
14.将方程x-2y=6变形为用含y的式子表示x,那么x= .
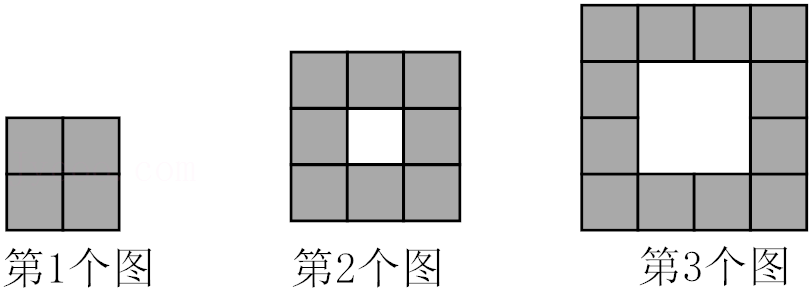
15.如图所示都是由若干朵大小相同的大丽花按照一定的规律摆成的,按照此规律下去,第n个图形中有 朵大丽花(用含n的式子表示).

16.(1)计算:(
)2×8-(-1)3÷(-
).
(2)下面是小艺同学解一元一次方程的过程,认真阅读并完成相应任务.
解方程:
-1=
.
解:去分母,得2(x-2)-1=3x.…第一步
去括号,得2x-4-1=3x.…第二步
移项,得2x-3x=1+4.…第三步
合并同类项,得-x=5.…第四步
系数化为1,得x=-5.…第五步
任务一:以上求解步骤中,第 步开始出现错误,错误原因是 .
任务二:该方程正确的解为 .
| 1 |
| 2 |
| 1 |
| 5 |
(2)下面是小艺同学解一元一次方程的过程,认真阅读并完成相应任务.
解方程:
| x-2 |
| 3 |
| x |
| 2 |
解:去分母,得2(x-2)-1=3x.…第一步
去括号,得2x-4-1=3x.…第二步
移项,得2x-3x=1+4.…第三步
合并同类项,得-x=5.…第四步
系数化为1,得x=-5.…第五步
任务一:以上求解步骤中,第 步开始出现错误,错误原因是 .
任务二:该方程正确的解为 .
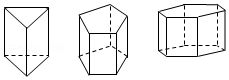
17.如图所示,是我们熟悉的三棱柱、五棱柱和六棱柱.
(1)填写下表:
(2)设n棱柱(n为正整数,且n≥3)的顶点数为a、棱数为b、面数为c,根据表中数据猜想a+c-b= .
(1)填写下表:
| 顶点数 | 面数 | 棱数 | |
| 三棱柱 | 5 | 9 | |
| 五棱柱 | 10 | 15 | |
| 六棱柱 | 8 |
(2)设n棱柱(n为正整数,且n≥3)的顶点数为a、棱数为b、面数为c,根据表中数据猜想a+c-b= .

18.在数学课上,王老师出示了这样一道题目:“当x=-
,y=-2022时,求多项式4x2-6xy-3y2-3(x2-2xy-y2-2x+
)的值.”解完这道题后,小明指出y=-2022是多余的条件.师生讨论后,一致认为小明的说法是正确的.请你说明正确的理由.
| 1 |
| 2 |
| 1 |
| 3 |
19.山西稷山板枣栽培历史有上千年,种类繁多,有板枣、长枣、圆枣等,以板枣最为有名.小明所在的小区购买了8筐稷山板枣,若以每筐10kg为基准,把超过10kg的千克数记为正数,不足10kg的千克数记为负数,记录如下:①+3;②-1.4;③+2;④-4;⑤+5;⑥-3.5;⑦+1;⑧-0.5.
(1)这8筐稷山板枣中,重量最重的是 kg,比重量最轻的重了 kg.
(2)这8筐稷山板枣的总重量是多少kg?

(1)这8筐稷山板枣中,重量最重的是 kg,比重量最轻的重了 kg.
(2)这8筐稷山板枣的总重量是多少kg?

20.阅读与思考
请阅读下列材料,并完成相应的任务:
任务:
(1)在图②中,若字母Q表示包装盒的上表面,字母P表示包装盒的侧面,则下表面在包装盒表面展开图中的位置是 ;
A.字母B B.字母A C.字母R D.字母T
(2)若在图③中,网格中每个小正方形的边长为1,求包装盒的表面积
请阅读下列材料,并完成相应的任务:
包装盒的展开图:如图①是一个同学们熟悉的包装盒,如图②是它的一种表面展开图,小明将图②画在如图③所示的8×8的网格中. |
任务:
(1)在图②中,若字母Q表示包装盒的上表面,字母P表示包装盒的侧面,则下表面在包装盒表面展开图中的位置是 ;
A.字母B B.字母A C.字母R D.字母T
(2)若在图③中,网格中每个小正方形的边长为1,求包装盒的表面积
21.对于有理数a,b,规定一种新运算:a*b=ab+b2.
(1)计算:(-5)*6.
(2)若方程
=
*2,求x的值.
(1)计算:(-5)*6.
(2)若方程
| x-1 |
| 2 |
| x-2 |
| 5 |
22.综合与实践
为抗击新冠肺炎疫情,某药店对消毒液和口罩开展优惠活动.消毒液每瓶定价25元,口罩每包定价8元,优惠方案有以下两种:①以定价购买时,买一瓶消毒液送一包口罩;②消毒液和口罩都按定价的80%付款.现某客户要到该药店购买消毒液40瓶,口罩x包(x>40).
(1)若该客户按方案①购买,需付款 元(用含x的式子表示);若该客户按方案②购买,需付款 元(用含x的式子表示并化简).
(2)若x=80,通过计算说明按方案①,方案②哪种方案购买较为省钱?
(3)试求当x取何值时,方案①和方案②的购买费用一样.
为抗击新冠肺炎疫情,某药店对消毒液和口罩开展优惠活动.消毒液每瓶定价25元,口罩每包定价8元,优惠方案有以下两种:①以定价购买时,买一瓶消毒液送一包口罩;②消毒液和口罩都按定价的80%付款.现某客户要到该药店购买消毒液40瓶,口罩x包(x>40).

(1)若该客户按方案①购买,需付款 元(用含x的式子表示);若该客户按方案②购买,需付款 元(用含x的式子表示并化简).
(2)若x=80,通过计算说明按方案①,方案②哪种方案购买较为省钱?
(3)试求当x取何值时,方案①和方案②的购买费用一样.
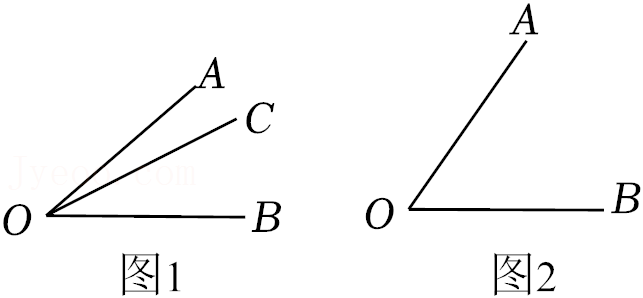
23.如图1,在∠AOB的内部画射线OC,射线OC把∠AOB分成两个角,分别为∠AOC和∠BOC,若这两个角中有一个角是另外一个角的2倍,则称射线OC为∠AOB的“3等分线”.
(1)若∠AOB=90°,射线OC为∠AOB的“3等分线”,则∠AOC的度数为 .
(2)如图2,∠AOB=60°,过点O在∠AOB外部作射线OP.若OA,OP,OB三条射线中,一条射线恰好是以另外两条射线为角的“3等分线”,求∠AOP(∠AOP≤180°)的度数.
(1)若∠AOB=90°,射线OC为∠AOB的“3等分线”,则∠AOC的度数为 .
(2)如图2,∠AOB=60°,过点O在∠AOB外部作射线OP.若OA,OP,OB三条射线中,一条射线恰好是以另外两条射线为角的“3等分线”,求∠AOP(∠AOP≤180°)的度数.

查看全部题目
相关试卷推荐
更多热门试卷
如何查看答案以及解析
扫描右侧二维码查看试卷答案解析以及视频讲解