下载高清试卷
【2021-2022学年河南省信阳市浉河区七年级(上)期末数学试卷】-第1页
试卷格式:2021-2022学年河南省信阳市浉河区七年级(上)期末数学试卷.PDF
试卷热词:最新试卷、2022年、河南试卷、信阳市试卷、数学试卷、七年级上学期试卷、期末试卷、初中试卷

扫码查看解析
试卷题目
1.中国人很早就开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入了负数.如果支出150元记作-150元,那么+80元表示( )


- A. 收入80元
- B. 支出80元
- C. 收入20元
- D. 支出20元
2.若单项式2xy3-b是三次单项式,则( )
- A. b=0
- B. b=1
- C. b=2
- D. b=3
3.下列计算错误的是( )
- A. -3-5=-8
- B. 3÷9×(-)=-3
1 9 - C. 8÷(-)=-32
1 4 - D. 3×23=24
4.多项式1+2xy-3xy2的次数及最高次项的系数分别是( )
- A. 3,-3
- B. 2,-3
- C. 5,-3
- D. 3,1
5.科学防疫从勤洗手开始,一双没洗干净的手上带有各种细菌病毒大约850000000个,这个数据用科学记数法表示为( )
- A. 0.85×109
- B. 8.5×107
- C. 8.5×108
- D. 85×107
6.把如图所示的纸片沿着虚线折叠,可以得到的几何体是( )
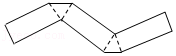

- A. 三棱柱
- B. 四棱柱
- C. 三棱锥
- D. 四棱锥
7.已知关于x的一元一次方程(k-2)x+2=0的解是x=2,则k的值为( )
- A. -1
- B. 0
- C. 1
- D. 2
8.某商品的进价是500元,标价是750元,商店要求以利润率为5%的售价打折出售,售货员可以打几折出售此商品( )
- A. 5
- B. 6
- C. 7
- D. 8
9.将三角尺与直尺按如图所示摆放,下列关于∠α与∠β之间的关系一定正确的是( )
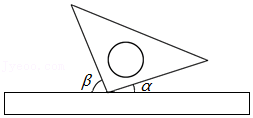

- A. ∠α=∠β
- B. ∠α=∠β
1 2 - C. ∠α+∠β=90°
- D. ∠α+∠β=180°
10.观察如图图形及图形所对的算式,根据你发现的规律计算1+8+16+24+…+8n(n为正整数)的结果( )


- A. n2
- B. (2n-1)2
- C. (n+2)2
- D. (2n+1)2
11.近似数2.8万精确到 位.
12.如果单项式-xyb+1与
xa-2y3是同类项,那么(b-a)2021= .
| 1 |
| 2 |
13.已知∠α=35°40',则∠α的补角的度数为 .
14.表示有理数a,b,c的点在数轴上的位置如图所示,请化简:|c+b-a|-|a-b|= .
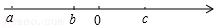
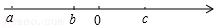
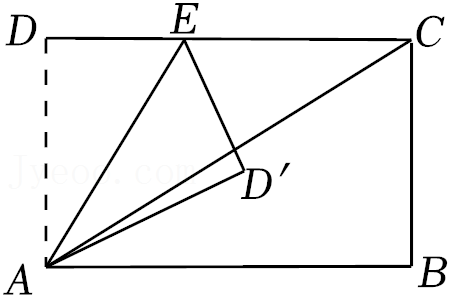
15.如图,把一张长方形纸片ABCD的一角沿AE折叠,点D的对应点D'落在∠BAC的内部,若∠CAE=2∠BAD',且∠CAD'=15°,则∠DAE的度数为 .

16.计算:
(1)-14+(-1)2021×(3-5);
(2)
-2=1+
.
(1)-14+(-1)2021×(3-5);
(2)
| x+1 |
| 2 |
| 2-x |
| 4 |
17.先化简,再求值:6(2a2b-ab2)-3(-ab2+4a2b),其中a,b的值满足|a-2|+(b+3)2=0.
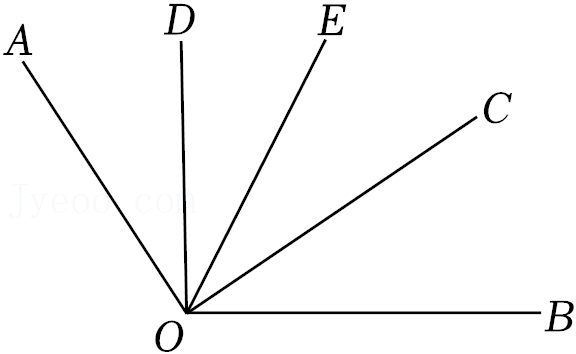
18.如图,∠AOC和∠BOD都是直角.
(1)判断∠COB与图中哪个角相等;
(2)若∠DOC=70°,过点O作∠AOB的平分线OE,则∠AOE的度数为________,并简单写出求解过程.
(1)判断∠COB与图中哪个角相等;
(2)若∠DOC=70°,过点O作∠AOB的平分线OE,则∠AOE的度数为________,并简单写出求解过程.

19.如图,已知B、C在线段AD上.

(1)图中共有 条线段;
(2)若AB=CD.
①比较线段的大小:AC BD(填:“>”、“=”或“<”);
②若AD=20,BC=12,M是AB的中点,N是CD的中点,求MN的长度.


(1)图中共有 条线段;
(2)若AB=CD.
①比较线段的大小:AC BD(填:“>”、“=”或“<”);
②若AD=20,BC=12,M是AB的中点,N是CD的中点,求MN的长度.

20.为抗击新冠肺炎疫情,某药店对消毒液和口罩开展优惠活动.消毒液每瓶定价10元,口罩每包定价5元,优惠方案有以下两种:①以定价购买时,买一瓶消毒液送一包口罩;②消毒液和口罩都按定价的80%付款.现某客户要到该药店购买消毒液30瓶,口罩x包(x>30).
(1)若该客户按方案①购买需付款 元(用含x的式子表示);若该客户按方案②购买需付款 元(用含x的式子表示);
(2)若x=50时,通过计算说明按方案①,方案②哪种方案购买较为省钱?
(3)试求当x取何值时,方案①和方案②的购买费用一样.
(1)若该客户按方案①购买需付款 元(用含x的式子表示);若该客户按方案②购买需付款 元(用含x的式子表示);
(2)若x=50时,通过计算说明按方案①,方案②哪种方案购买较为省钱?
(3)试求当x取何值时,方案①和方案②的购买费用一样.
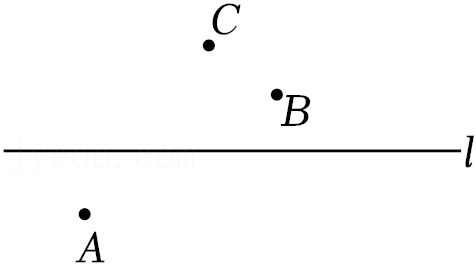
21.如图,已知直线l和直线外三点A、B、C,按下列要求画图:
(1)画射线AB;
(2)画线段BC;
(3)用圆规在BC延长线上截取CD=BC;
(4)在直线l上确定点E,使得AE+CE最小,并说明你的作图依据 .
(1)画射线AB;
(2)画线段BC;
(3)用圆规在BC延长线上截取CD=BC;
(4)在直线l上确定点E,使得AE+CE最小,并说明你的作图依据 .

22.阅读材料:
“整体思想”是中学数学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛,如我们把(a+b)看成一个整体,则4(a+b)-2(a+b)+(a+b)=(4-2+1)(a+b)=3(a+b).
(1)尝试应用:
把(a-b)2看成一个整体,合并3(a-b)2-6(a-b)2+7(a-b)2的结果是 ;
(2)拓广探索:
已知x2+2y=-
,求-6y-3x2+2021的值.
“整体思想”是中学数学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛,如我们把(a+b)看成一个整体,则4(a+b)-2(a+b)+(a+b)=(4-2+1)(a+b)=3(a+b).
(1)尝试应用:
把(a-b)2看成一个整体,合并3(a-b)2-6(a-b)2+7(a-b)2的结果是 ;
(2)拓广探索:
已知x2+2y=-
| 1 |
| 3 |
23.新定义问题
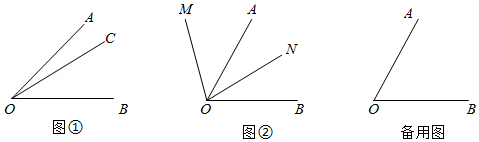
如图①,已知∠AOB,在∠AOB内部画射线OC,得到三个角,分别为∠AOC、∠BOC、∠AOB.若这三个角中有一个角是另外一个角的2倍,则称射线OC为∠AOB的“幸运线”.(本题中所研究的角都是大于0°而小于180°的角.)
【阅读理解】
(1)角的平分线 这个角的“幸运线”;(填“是”或“不是”)
【初步应用】
(2)如图①,∠AOB=45°,射线OC为∠AOB的“幸运线”,则∠AOC的度数为 ;
【解决问题】
(3)如图②,已知∠AOB=60°,射线OM从OA出发,以每秒20°的速度绕O点逆时针旋转,同时,射线ON从OB出发,以每秒15°的速度绕O点逆时针旋转,设运动的时间为t秒(0<t<9).若OM、ON、OA三条射线中,一条射线恰好是以另外两条射线为边的角的“幸运线”,求出所有可能的t值.
如图①,已知∠AOB,在∠AOB内部画射线OC,得到三个角,分别为∠AOC、∠BOC、∠AOB.若这三个角中有一个角是另外一个角的2倍,则称射线OC为∠AOB的“幸运线”.(本题中所研究的角都是大于0°而小于180°的角.)

【阅读理解】
(1)角的平分线 这个角的“幸运线”;(填“是”或“不是”)
【初步应用】
(2)如图①,∠AOB=45°,射线OC为∠AOB的“幸运线”,则∠AOC的度数为 ;
【解决问题】
(3)如图②,已知∠AOB=60°,射线OM从OA出发,以每秒20°的速度绕O点逆时针旋转,同时,射线ON从OB出发,以每秒15°的速度绕O点逆时针旋转,设运动的时间为t秒(0<t<9).若OM、ON、OA三条射线中,一条射线恰好是以另外两条射线为边的角的“幸运线”,求出所有可能的t值.
查看全部题目
相关试卷推荐
更多热门试卷
如何查看答案以及解析
扫描右侧二维码查看试卷答案解析以及视频讲解