下载高清试卷
【2022年江苏省苏州市中考数学试卷】-第1页
试卷格式:2022年江苏省苏州市中考数学试卷.PDF
试卷热词:最新试卷、2022年、江苏试卷、苏州市试卷、数学试卷、九年级试卷、中考试卷、初中试卷
扫码查看解析
试卷题目
1.下列实数中,比3大的数是( )
- A. 5
- B. 1
- C. 0
- D. -2
2.2022年1月17日,国务院新闻办公室公布:截至2021年末全国人口总数为141260万,比上年末增加48万人,中国人口的增长逐渐缓慢.141260用科学记数法可表示为( )
- A. 0.14126×106
- B. 1.4126×106
- C. 1.4126×105
- D. 14.126×104
3.下列运算正确的是( )
- A. √(-7)2=-7
- B. 6÷=9
2 3 - C. 2a+2b=2ab
- D. 2a•3b=5ab
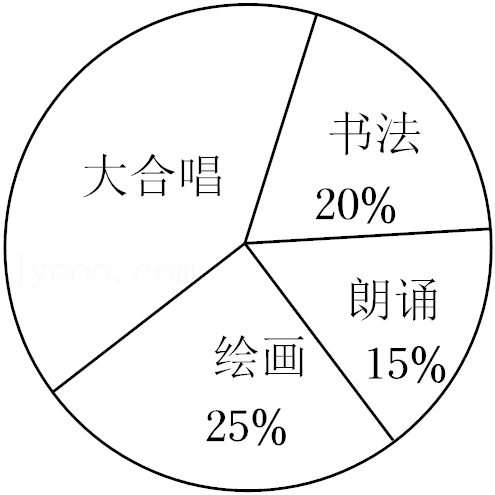
4.为迎接党的二十大胜利召开,某校开展了“学党史,悟初心”系列活动.学校对学生参加各项活动的人数进行了调查,并将数据绘制成如下统计图.若参加“书法”的人数为80人,则参加“大合唱”的人数为( )

- A. 60人
- B. 100人
- C. 160人
- D. 400人
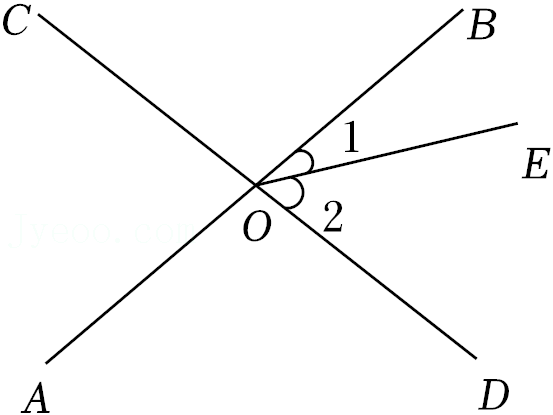
5.如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是( )

- A. 25°
- B. 30°
- C. 40°
- D. 50°
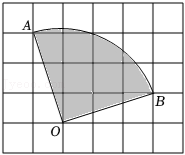
6.如图,在5×6的长方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点,扇形OAB的圆心及弧的两端均为格点.假设飞镖击中每一块小正方形是等可能的(击中扇形的边界或没有击中游戏板,则重投1次),任意投掷飞镖1次,飞镖击中扇形OAB(阴影部分)的概率是( )

- A.
π 12 - B.
π 24 - C. √10π
60 - D. √5π
60
7.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术,其中方程术是其最高的代数成就.《九章算术》中有这样一个问题:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?”译文:“相同时间内,走路快的人走100步,走路慢的人只走60步.若走路慢的人先走100步,走路快的人要走多少步才能追上?(注:步为长度单位)”设走路快的人要走x步才能追上,根据题意可列出的方程是( )
- A. x=100-x
60 100 - B. x=100+x
60 100 - C. x=100+x
100 60 - D. x=100-x
100 60
8.如图,点A的坐标为(0,2),点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60°得到线段AC.若点C的坐标为(m,3),则m的值为( )


- A.
4 √33 - B.
2 √213 - C.
5 √33 - D.
4 √213
9.计算:a•a3= .
10.已知x+y=4,x-y=6,则x2-y2= .
11.化简
-
的结果是 .
| x2 |
| x-2 |
| 2x |
| x-2 |
12.定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰△ABC是“倍长三角形”,底边BC的长为3,则腰AB的长为 .
13.如图,AB是⊙O的直径,弦CD交AB于点E,连接AC,AD.若∠BAC=28°,则∠D= °.
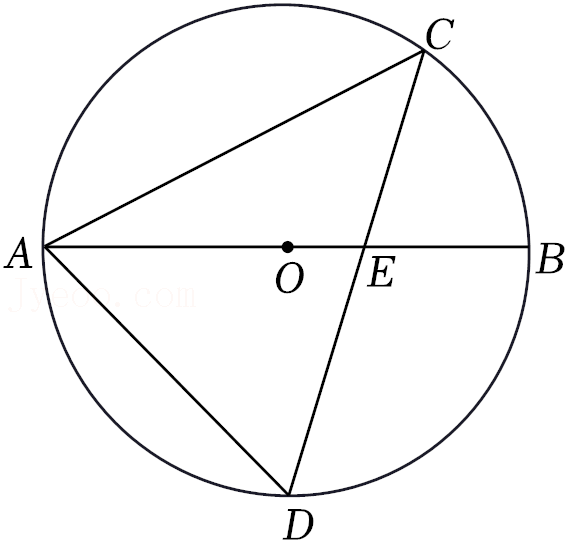

14.如图,在平行四边形ABCD中,AB⊥AC,AB=3,AC=4,分别以A,C为圆心,大于
AC的长为半径画弧,两弧相交于点M,N,过M,N两点作直线,与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为 .

| 1 |
| 2 |

15.一个装有进水管和出水管的容器,开始时,先打开进水管注水,3分钟时,再打开出水管排水,8分钟时,关闭进水管,直至容器中的水全部排完.在整个过程中,容器中的水量y(升)与时间x(分钟)之间的函数关系如图所示,则图中a的值为 .


16.如图,在矩形ABCD中,
=
.动点M从点A出发,沿边AD向点D匀速运动,动点N从点B出发,沿边BC向点C匀速运动,连接MN.动点M,N同时出发,点M运动的速度为v1,点N运动的速度为v2,且v1<v2.当点N到达点C时,M,N两点同时停止运动.在运动过程中,将四边形MABN沿MN翻折,得到四边形MA′B′N.若在某一时刻,点B的对应点B′恰好与CD的中点重合,则
的值为 .
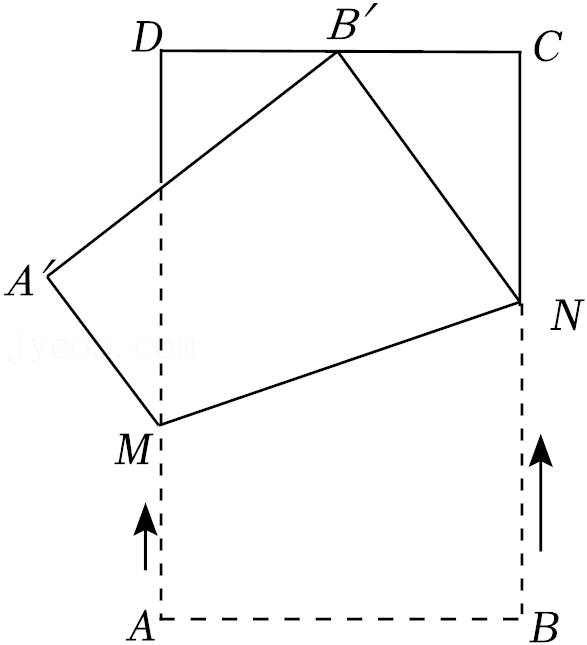
| AB |
| BC |
| 2 |
| 3 |
| v1 |
| v2 |

17.计算:|-3|+22-(
√3
-1)0.18.解方程:
+
=1.
| x |
| x+1 |
| 3 |
| x |
19.已知3x2-2x-3=0,求(x-1)2+x(x+
)的值.
| 2 |
| 3 |
20.一只不透明的袋子中装有1个白球,3个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出1个球,这个球是白球的概率为 ;
(2)搅匀后从中任意摸出1个球,记录颜色后放回,搅匀,再从中任意摸出1个球,求2次摸到的球恰好是1个白球和1个红球的概率.(请用画树状图或列表等方法说明理由)
(1)搅匀后从中任意摸出1个球,这个球是白球的概率为 ;
(2)搅匀后从中任意摸出1个球,记录颜色后放回,搅匀,再从中任意摸出1个球,求2次摸到的球恰好是1个白球和1个红球的概率.(请用画树状图或列表等方法说明理由)
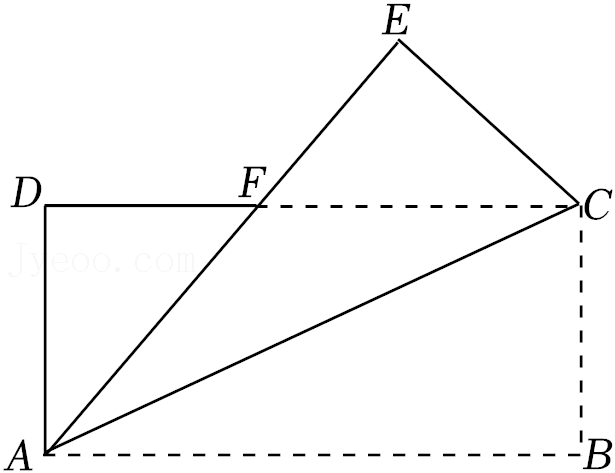
21.如图,将矩形ABCD沿对角线AC折叠,点B的对应点为点E,AE与CD交于点F.
(1)求证:△DAF≌△ECF;
(2)若∠FCE=40°,求∠CAB的度数.
(1)求证:△DAF≌△ECF;
(2)若∠FCE=40°,求∠CAB的度数.

22.某校九年级640名学生在“信息素养提升”培训前、后各参加了一次水平相同的测试,并以同一标准折算成“6分”、“7分”、“8分”、“9分”、“10分”5个成绩.为了解培训效果,用抽样调查的方式从中抽取了32名学生的2次测试成绩,并用划记法制成了如表表格:
(1)这32名学生2次测试成绩中,培训前测试成绩的中位数是m,培训后测试成绩的中位数是n,则m n;(填“>”、“<”或“=”)
(2)这32名学生经过培训,测试成绩为“6分”的百分比比培训前减少了多少?
(3)估计该校九年级640名学生经过培训,测试成绩为“10分”的学生增加了多少人?
| 培训前 | 成绩(分) | 6 | 7 | 8 | 9 | 10 |
| 划记 |  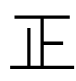 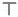 | 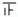 | 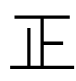 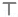 | 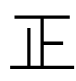 | 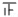 | |
| 人数(人) | 12 | 4 | 7 | 5 | 4 | |
| 培训后 | 成绩(分) | 6 | 7 | 8 | 9 | 10 |
| 划记 | 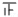 | 一 | 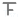 | 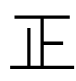 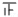 | 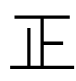   | |
| 人数(人) | 4 | 1 | 3 | 9 | 15 |
(1)这32名学生2次测试成绩中,培训前测试成绩的中位数是m,培训后测试成绩的中位数是n,则m n;(填“>”、“<”或“=”)
(2)这32名学生经过培训,测试成绩为“6分”的百分比比培训前减少了多少?
(3)估计该校九年级640名学生经过培训,测试成绩为“10分”的学生增加了多少人?
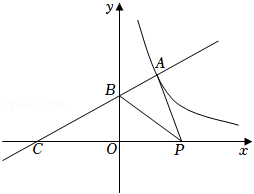
23.如图,一次函数y=kx+2(k≠0)的图象与反比例函数y=
(m≠0,x>0)的图象交于点A(2,n),与y轴交于点B,与x轴交于点C(-4,0).
(1)求k与m的值;
(2)P(a,0)为x轴上的一动点,当△APB的面积为
时,求a的值.
| m |
| x |
(1)求k与m的值;
(2)P(a,0)为x轴上的一动点,当△APB的面积为
| 7 |
| 2 |

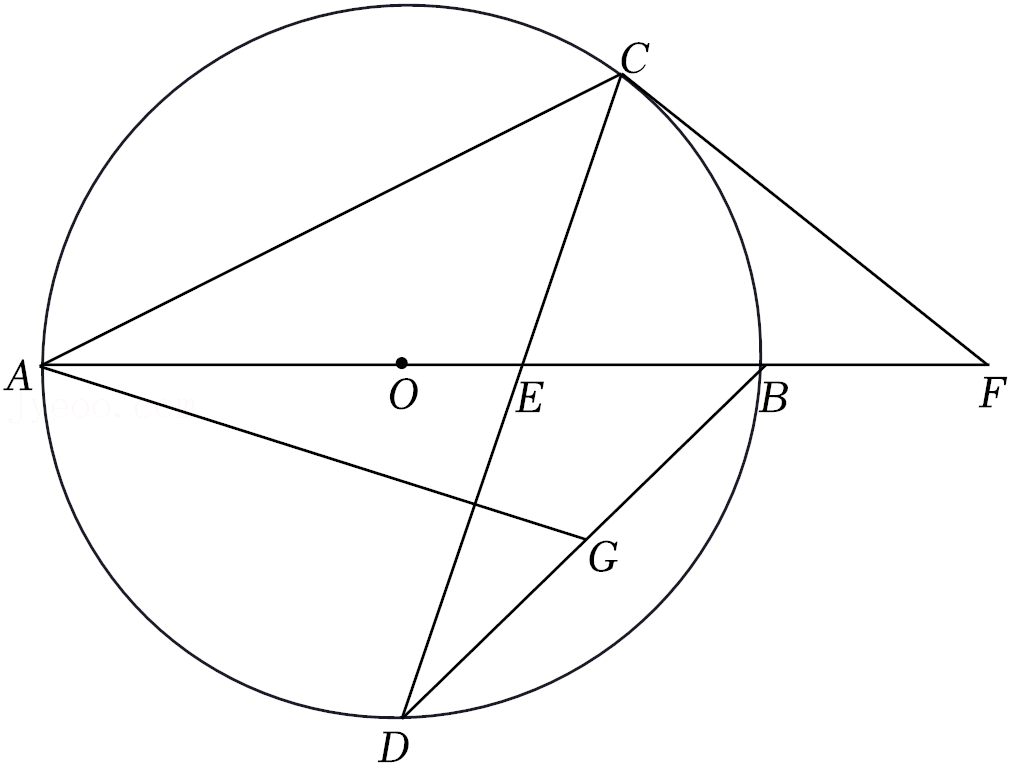
24.如图,AB是⊙O的直径,AC是弦,D是⌒AB的中点,CD与AB交于点E.F是AB延长线上的一点,且CF=EF.
(1)求证:CF为⊙O的切线;
(2)连接BD,取BD的中点G,连接AG.若CF=4,BF=2,求AG的长.
(1)求证:CF为⊙O的切线;
(2)连接BD,取BD的中点G,连接AG.若CF=4,BF=2,求AG的长.

25.某水果店经销甲、乙两种水果,两次购进水果的情况如表所示:
(1)求甲、乙两种水果的进价;
(2)销售完前两次购进的水果后,该水果店决定回馈顾客,开展促销活动.第三次购进甲、乙两种水果共200千克,且投入的资金不超过3360元.将其中的m千克甲种水果和3m千克乙种水果按进价销售,剩余的甲种水果以每千克17元、乙种水果以每千克30元的价格销售.若第三次购进的200千克水果全部售出后,获得的最大利润不低于800元,求正整数m的最大值.
| 进货批次 | 甲种水果质量(单位:千克) | 乙种水果质量(单位:千克) | 总费用(单位:元) |
| 第一次 | 60 | 40 | 1520 |
| 第二次 | 30 | 50 | 1360 |
(1)求甲、乙两种水果的进价;
(2)销售完前两次购进的水果后,该水果店决定回馈顾客,开展促销活动.第三次购进甲、乙两种水果共200千克,且投入的资金不超过3360元.将其中的m千克甲种水果和3m千克乙种水果按进价销售,剩余的甲种水果以每千克17元、乙种水果以每千克30元的价格销售.若第三次购进的200千克水果全部售出后,获得的最大利润不低于800元,求正整数m的最大值.
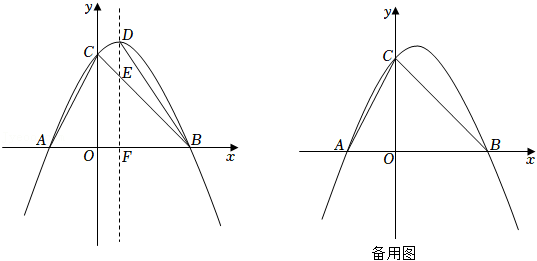
26.如图,二次函数y=-x2+2mx+2m+1(m是常数,且m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.其对称轴与线段BC交于点E,与x轴交于点F.连接AC,BD.
(1)求A,B,C三点的坐标(用数字或含m的式子表示),并求∠OBC的度数;
(2)若∠ACO=∠CBD,求m的值;
(3)若在第四象限内二次函数y=-x2+2mx+2m+1(m是常数,且m>0)的图象上,始终存在一点P,使得∠ACP=75°,请结合函数的图象,直接写出m的取值范围.
(1)求A,B,C三点的坐标(用数字或含m的式子表示),并求∠OBC的度数;
(2)若∠ACO=∠CBD,求m的值;
(3)若在第四象限内二次函数y=-x2+2mx+2m+1(m是常数,且m>0)的图象上,始终存在一点P,使得∠ACP=75°,请结合函数的图象,直接写出m的取值范围.

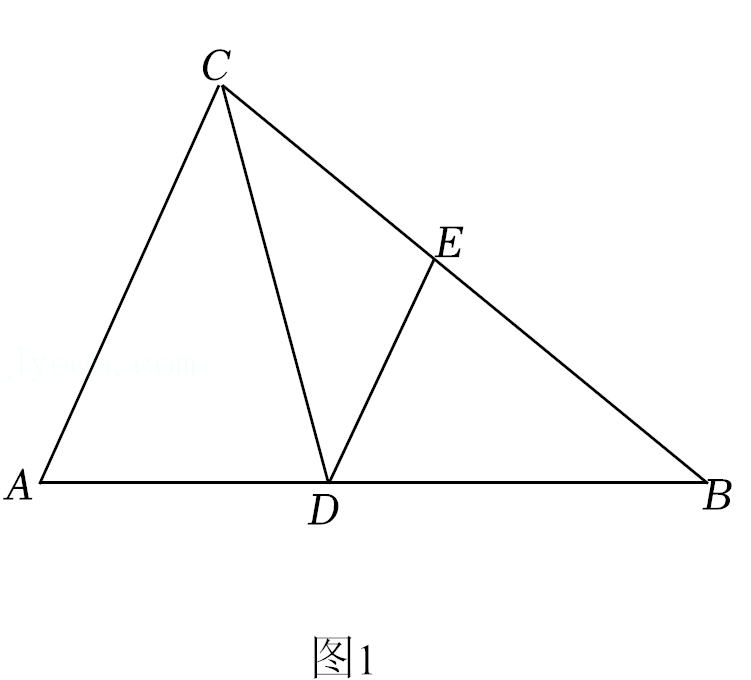
27.(1)如图1,在△ABC中,∠ACB=2∠B,CD平分∠ACB,交AB于点D,DE∥AC,交BC于点E.
①若DE=1,BD=
,求BC的长;
②试探究
-
是否为定值.如果是,请求出这个定值;如果不是,请说明理由.
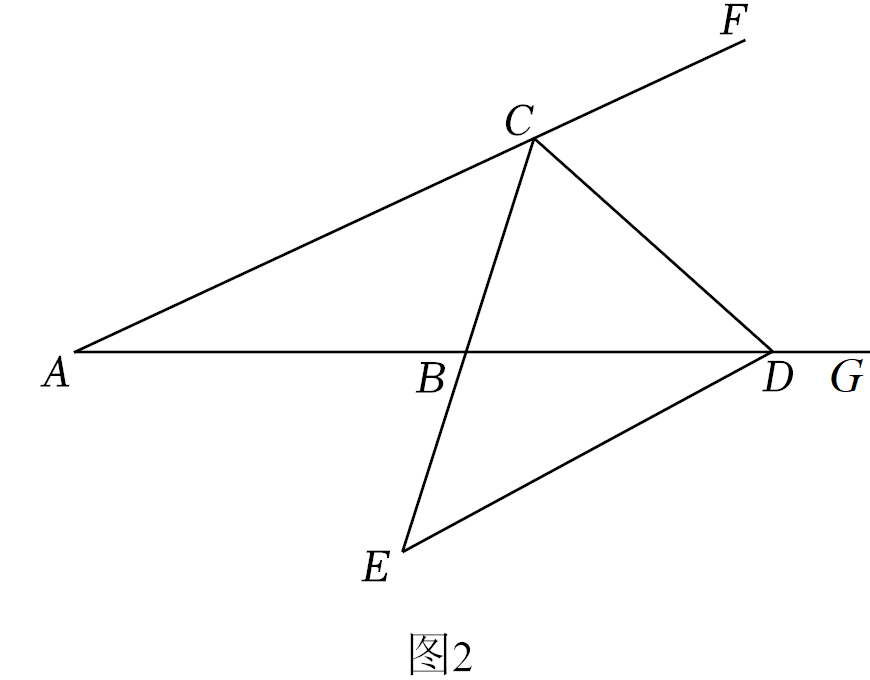
(2)如图2,∠CBG和∠BCF是△ABC的2个外角,∠BCF=2∠CBG,CD平分∠BCF,交AB的延长线于点D,DE∥AC,交CB的延长线于点E.记△ACD的面积为S1,△CDE的面积为S2,△BDE的面积为S3.若S1•S3=
S22,求cos∠CBD的值.
①若DE=1,BD=
| 3 |
| 2 |
②试探究
| AB |
| AD |
| BE |
| DE |
(2)如图2,∠CBG和∠BCF是△ABC的2个外角,∠BCF=2∠CBG,CD平分∠BCF,交AB的延长线于点D,DE∥AC,交CB的延长线于点E.记△ACD的面积为S1,△CDE的面积为S2,△BDE的面积为S3.若S1•S3=
| 9 |
| 16 |


查看全部题目