下载高清试卷
【2022年广西贵港市中考数学试卷】-第1页
试卷格式:2022年广西贵港市中考数学试卷.PDF
试卷热词:最新试卷、2022年、广西试卷、贵港市试卷、数学试卷、九年级试卷、中考试卷、初中试卷

扫码查看解析
试卷题目
1.-2的倒数是( )
- A. 2
- B. -2
- C.
1 2 - D. -
1 2
2.一个圆锥如图所示放置,对于它的三视图,下列说法正确的是( )
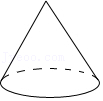

- A. 主视图与俯视图相同
- B. 主视图与左视图相同
- C. 左视图与俯视图相同
- D. 三个视图完全相同
3.一组数据3,5,1,4,6,5的众数和中位数分别是( )
- A. 5,4.5
- B. 4.5,4
- C. 4,4.5
- D. 5,5
4.据报道:芯片被誉为现代工业的掌上明珠,芯片制造的核心是光刻技术,我国的光刻技术水平已突破到28nm.已知1nm=10-9m,则28nm用科学记数法表示是( )
- A. 28×10-9m
- B. 2.8×10-9m
- C. 2.8×10-8m
- D. 2.8×10-10m
5.下列计算正确的是( )
- A. 2a-a=2
- B. a2+b2=a2b2
- C. (-2a)3=8a3
- D. (-a3)2=a6
6.若点A(a,-1)与点B(2,b)关于y轴对称,则a-b的值是( )
- A. -1
- B. -3
- C. 1
- D. 2
7.若x=-2是一元二次方程x2+2x+m=0的一个根,则方程的另一个根及m的值分别是( )
- A. 0,-2
- B. 0,0
- C. -2,-2
- D. -2,0
8.下列命题为真命题的是( )
- A. √a2=a
- B. 同位角相等
- C. 三角形的内心到三边的距离相等
- D. 正多边形都是中心对称图形
9.如图,⊙O是△ABC的外接圆,AC是⊙O的直径,点P在⊙O上,若∠ACB=40°,则∠BPC的度数是( )
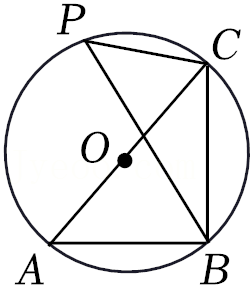

- A. 40°
- B. 45°
- C. 50°
- D. 55°
10.如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=16m,则这棵树CD的高度是( )
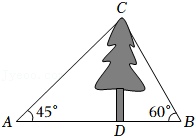

- A. 8(3-√3)m
- B. 8(3+√3)m
- C. 6(3-√3)m
- D. 6(3+√3)m
11.如图,在4×4网格正方形中,每个小正方形的边长为1,顶点为格点,若△ABC的顶点均是格点,则cos∠BAC的值是( )
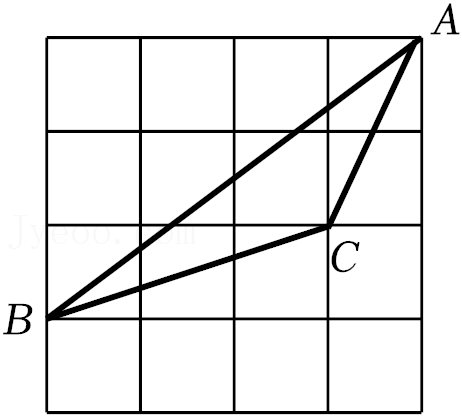

- A. √5
5 - B. √10
5 - C.
2 √55 - D.
4 5
12.如图,在边长为1的菱形ABCD中,∠ABC=60°,动点E在AB边上(与点A,B均不重合),点F在对角线AC上,CE与BF相交于点G,连接AG,DF,若AF=BE,则下列结论错误的是( )
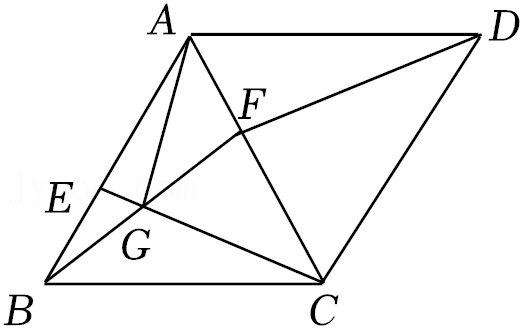

- A. DF=CE
- B. ∠BGC=120°
- C. AF2=EG•EC
- D. AG的最小值为
2 √23
13.若
√x+1
在实数范围内有意义,则实数x的取值范围是 .14.因式分解:a3-a= .
15.从-3,-2,2这三个数中任取两个不同的数,作为点的坐标,则该点落在第三象限的概率是 .
16.如图,将△ABC绕点A逆时针旋转角α(0°<α<180°)得到△ADE,点B的对应点D恰好落在BC边上,若DE⊥AC,∠CAD=25°,则旋转角α的度数是 .
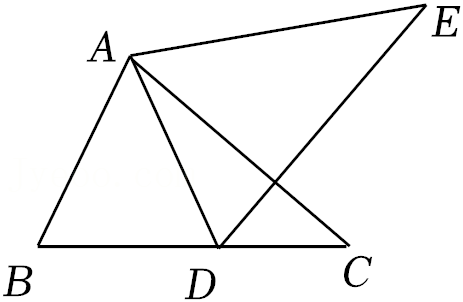

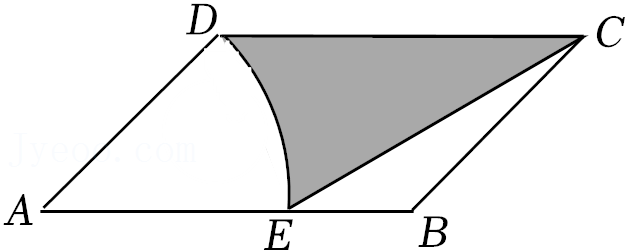
17.如图,在▱ABCD中,AD=
AB,∠BAD=45°,以点A为圆心、AD为半径画弧交AB于点E,连接CE,若AB=3
| 2 |
| 3 |
√2
,则图中阴影部分的面积是 .
18.已知二次函数y=ax2+bx+c(a≠0)图象的一部分如图所示,该函数图象经过点(-2,0),对称轴为直线x=-
.对于下列结论:①abc<0;②b2-4ac>0;③a+b+c=0;④am2+bm<
(a-2b)(其中m≠-
);⑤若A(x1,y1)和B(x2,y2)均在该函数图象上,且x1>x2>1,则y1>y2.其中正确结论的个数共有 个.

| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |

19.(1)计算:|1-
)-2-tan60°;
(2)解不等式组:
√3
|+(2022-π)0+(-| 1 |
| 2 |
(2)解不等式组:
| { |
|
20.尺规作图(保留作图痕迹,不要求写出作法):
如图,已知线段m,n.求作△ABC,使∠A=90°,AB=m,BC=n.
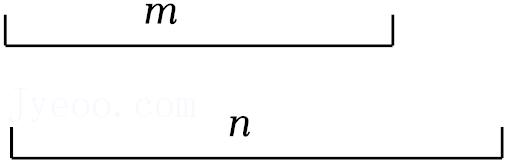
如图,已知线段m,n.求作△ABC,使∠A=90°,AB=m,BC=n.
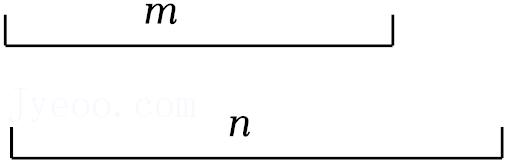
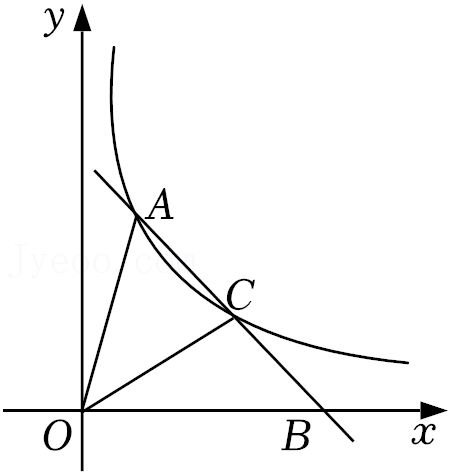
21.如图,直线AB与反比例函数y=
(k>0,x>0)的图象相交于点A和点C(3,2),与x轴的正半轴相交于点B.
(1)求k的值;
(2)连接OA,OC,若点C为线段AB的中点,求△AOC的面积.
| k |
| x |
(1)求k的值;
(2)连接OA,OC,若点C为线段AB的中点,求△AOC的面积.

22.在贯彻落实“五育并举”的工作中,某校开设了五个社团活动:传统国学(A)、科技兴趣(B)、民族体育(C)、艺术鉴赏(D)、劳技实践(E),每个学生每个学期只参加一个社团活动.为了了解本学期学生参加社团活动的情况,学校随机抽取了若干名学生进行调查,并将调查结果绘制成如下两幅尚不完整的统计图.请根据统计图提供的信息,解答下列问题:
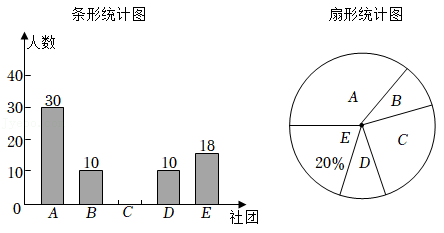
(1)本次调查的学生共有 人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,传统国学(A)对应扇形的圆心角度数是 ;
(4)若该校有2700名学生,请估算本学期参加艺术鉴赏(D)活动的学生人数.

(1)本次调查的学生共有 人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,传统国学(A)对应扇形的圆心角度数是 ;
(4)若该校有2700名学生,请估算本学期参加艺术鉴赏(D)活动的学生人数.
23.为了加强学生的体育锻炼,某班计划购买部分绳子和实心球.已知每条绳子的价格比每个实心球的价格少23元,且84元购买绳子的数量与360元购买实心球的数量相同.
(1)绳子和实心球的单价各是多少元?
(2)如果本次购买的总费用为510元,且购买绳子的数量是实心球数量的3倍,那么购买绳子和实心球的数量各是多少?
(1)绳子和实心球的单价各是多少元?
(2)如果本次购买的总费用为510元,且购买绳子的数量是实心球数量的3倍,那么购买绳子和实心球的数量各是多少?
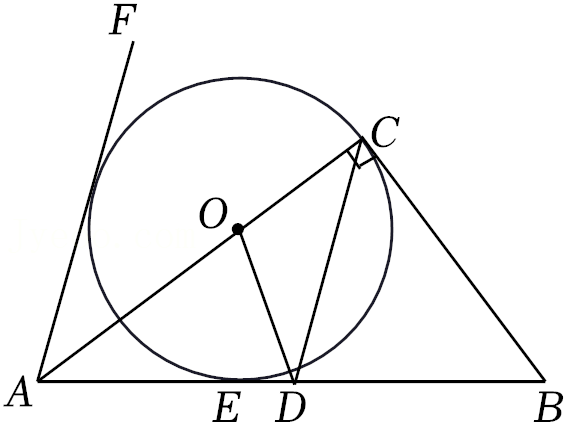
24.如图,在△ABC中,∠ACB=90°,点D是AB边的中点,点O在AC边上,⊙O经过点C且与AB边相切于点E,∠FAC=
∠BDC.
(1)求证:AF是⊙O的切线;
(2)若BC=6,sinB=
,求⊙O的半径及OD的长.
| 1 |
| 2 |
(1)求证:AF是⊙O的切线;
(2)若BC=6,sinB=
| 4 |
| 5 |

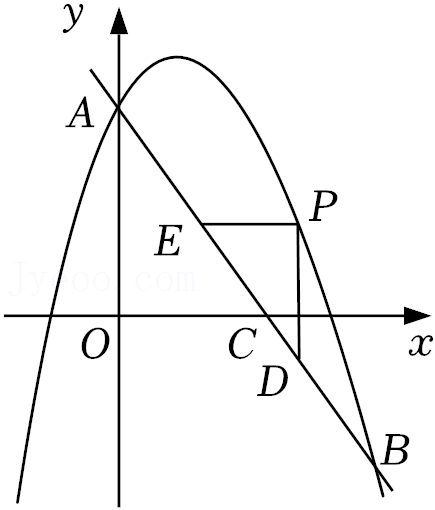
25.如图,已知抛物线y=-x2+bx+c经过A(0,3)和B(
,-
)两点,直线AB与x轴相交于点C,P是直线AB上方的抛物线上的一个动点,PD⊥x轴交AB于点D.
(1)求该抛物线的表达式;
(2)若PE∥x轴交AB于点E,求PD+PE的最大值;
(3)若以A,P,D为顶点的三角形与△AOC相似,请直接写出所有满足条件的点P,点D的坐标.
| 7 |
| 2 |
| 9 |
| 4 |
(1)求该抛物线的表达式;
(2)若PE∥x轴交AB于点E,求PD+PE的最大值;
(3)若以A,P,D为顶点的三角形与△AOC相似,请直接写出所有满足条件的点P,点D的坐标.

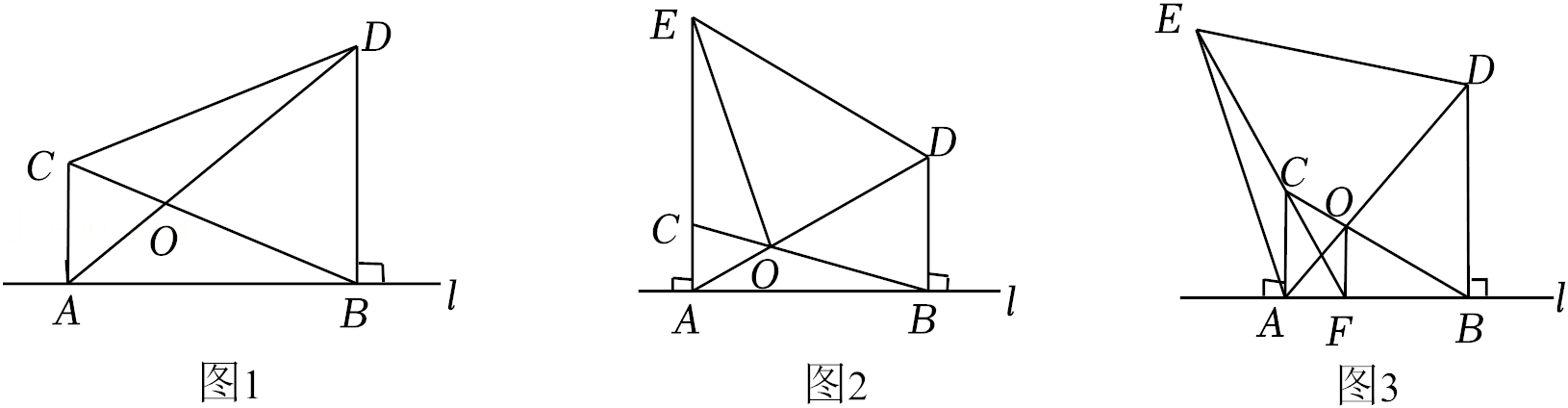
26.已知:点C,D均在直线l的上方,AC与BD都是直线l的垂线段,且BD在AC的右侧,BD=2AC,AD与BC相交于点O.
(1)如图1,若连接CD,则△BCD的形状为 ,
的值为 ;
(2)若将BD沿直线l平移,并以AD为一边在直线l的上方作等边△ADE.
①如图2,当AE与AC重合时,连接OE,若AC=
,求OE的长;
②如图3,当∠ACB=60°时,连接EC并延长交直线l于点F,连接OF.求证:OF⊥AB.
(1)如图1,若连接CD,则△BCD的形状为 ,
| AO |
| AD |
(2)若将BD沿直线l平移,并以AD为一边在直线l的上方作等边△ADE.
①如图2,当AE与AC重合时,连接OE,若AC=
| 3 |
| 2 |
②如图3,当∠ACB=60°时,连接EC并延长交直线l于点F,连接OF.求证:OF⊥AB.

查看全部题目