下载高清试卷
【2022年广西桂林市中考数学试卷】-第1页
试卷格式:2022年广西桂林市中考数学试卷.PDF
试卷热词:最新试卷、2022年、广西试卷、桂林市试卷、数学试卷、九年级试卷、中考试卷、初中试卷
扫码查看解析
试卷题目
1.在东西向的马路上,把出发点记为0,向东与向西意义相反.若把向东走2km记做“+2km”,那么向西走1km应记做( )
- A. -2km
- B. -1km
- C. 1km
- D. +2km
2.-3的绝对值是( )
- A. 3
- B.
1 3 - C. 0
- D. -3
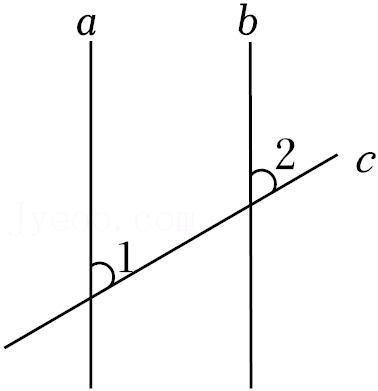
3.如图,直线a,b被直线c所截,且a∥b,若∠1=60°,则∠2的度数是( )

- A. 70°
- B. 60°
- C. 50°
- D. 40°
4.下列图形中,是中心对称图形的是( )
- A. 等边三角形
- B. 圆

- C. 正五边形
- D. 扇形
5.下列调查中,最适合采用全面调查的是( )
- A. 了解全国中学生的睡眠时间
- B. 了解某河流的水质情况
- C. 调查全班同学的视力情况
- D. 了解一批灯泡的使用寿命
6.2022年6月5日,中华民族再探苍穹,神舟十四号载人飞船通过长征二号F运载火箭成功升空,并与天和核心舱顺利进行接轨.据报道,长征二号F运载火箭的重量大约是500000kg.将数据500000用科学记数法表示,结果是( )
- A. 5×105
- B. 5×106
- C. 0.5×105
- D. 0.5×106
7.把不等式x-1<2的解集在数轴上表示出来,正确的是( )
- A.

- B.

- C.

- D.

8.化简
√12
的结果是( )- A. 2√3
- B. 3
- C. 2√2
- D. 2
9.桂林作为国际旅游名城,每年吸引着大量游客前来观光.现有一批游客分别乘坐甲乙两辆旅游大巴同时从旅行社前往某个旅游景点.行驶过程中甲大巴因故停留一段时间后继续驶向景点,乙大巴全程匀速驶向景点.两辆大巴的行程s(km)随时间t(h)变化的图象(全程)如图所示.依据图中信息,下列说法错误的是( )
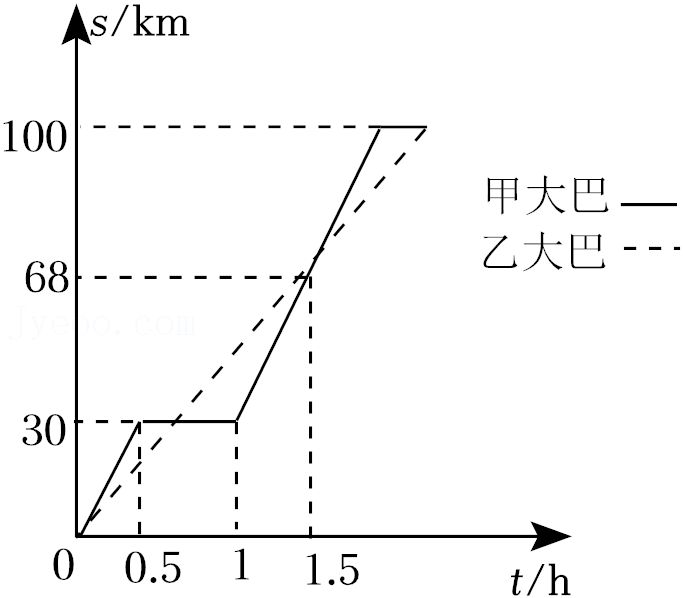

- A. 甲大巴比乙大巴先到达景点
- B. 甲大巴中途停留了0.5h
- C. 甲大巴停留后用1.5h追上乙大巴
- D. 甲大巴停留前的平均速度是60km/h
10.如图,在△ABC中,∠B=22.5°,∠C=45°,若AC=2,则△ABC的面积是( )
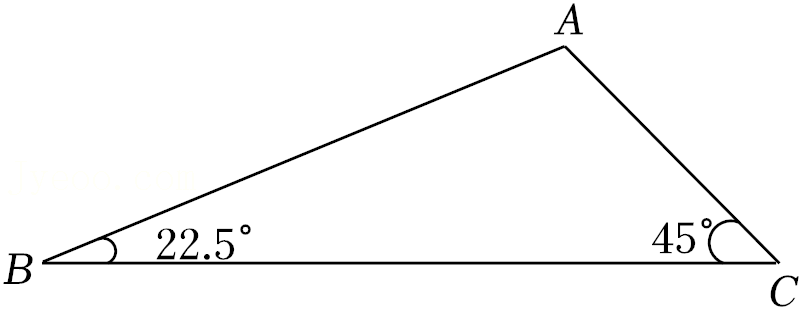

- A.
3+ √22 - B. 1+√2
- C. 2√2
- D. 2+√2
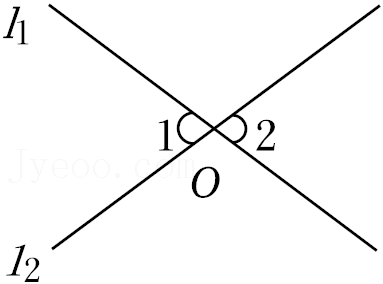
11.如图,直线l1,l2相交于点O,∠1=70°,则∠2= °.

12.如图,点C是线段AB的中点,若AC=2cm,则AB= cm.
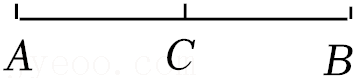
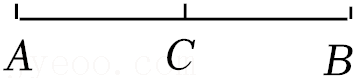
13.因式分解:a2+3a= .
14.当重复试验次数足够多时,可用频率来估计概率.历史上数学家皮尔逊(Pearson)曾在实验中掷均匀的硬币24000次,正面朝上的次数是12012次,频率约为0.5,则掷一枚均匀的硬币,正面朝上的概率是 .
15.如图,点A在反比例函数y=
的图象上,且点A的横坐标为a(a<0),AB⊥y轴于点B,若△AOB的面积是3,则k的值是 .

| k |
| x |

16.如图,某雕塑MN位于河段OA上,游客P在步道上由点O出发沿OB方向行走.已知∠AOB=30°,MN=2OM=40m,当观景视角∠MPN最大时,游客P行走的距离OP是 米.


17.计算:(-2)×0+5.
18.计算:tan45°-3-1.
19.解二元一次方程组:
.
| { |
|
20.如图,在平面直角坐标系中,形如英文字母“V”的图形三个端点的坐标分别是A(2,3),B(1,0),C(0,3).
(1)画出“V”字图形向左平移2个单位后的图形;
(2)画出原“V”字图形关于x轴对称的图形;
(3)所得图形与原图形结合起来,你能从中看出什么英文字母?(任意答一个即可)
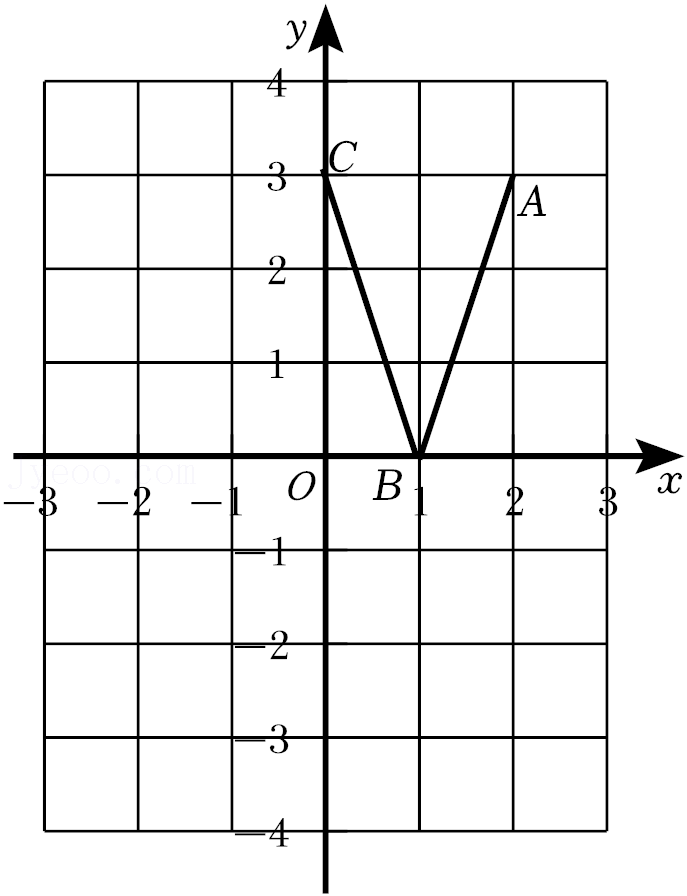
(1)画出“V”字图形向左平移2个单位后的图形;
(2)画出原“V”字图形关于x轴对称的图形;
(3)所得图形与原图形结合起来,你能从中看出什么英文字母?(任意答一个即可)

21.如图,在▱ABCD中,点E和点F是对角线BD上的两点,且BF=DE.
(1)求证:BE=DF;
(2)求证:△ABE≌△CDF.
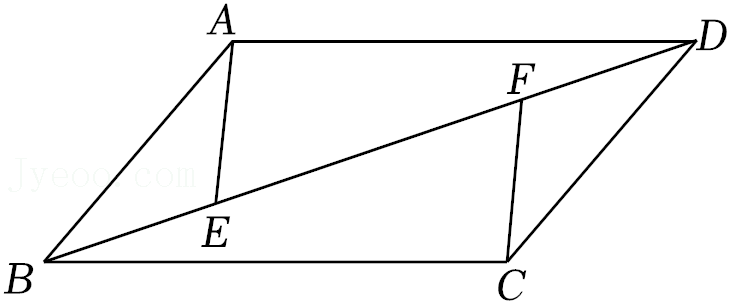
(1)求证:BE=DF;
(2)求证:△ABE≌△CDF.

22.某校将举办的“壮乡三月三”民族运动会中共有四个项目:A跳长绳,B抛绣球,C拔河,D跳竹竿舞.该校学生会围绕“你最喜欢的项目是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:
请结合统计图表,回答下列问题:
(1)填空:a= ;
(2)本次调查的学生总人数是多少?
(3)请将条形统计图补充完整;
(4)李红同学准备从抛绣球和跳竹竿舞两个项目中选择一项参加,但她拿不定主意,请你结合调查统计结果给她一些合理化建议进行选择.
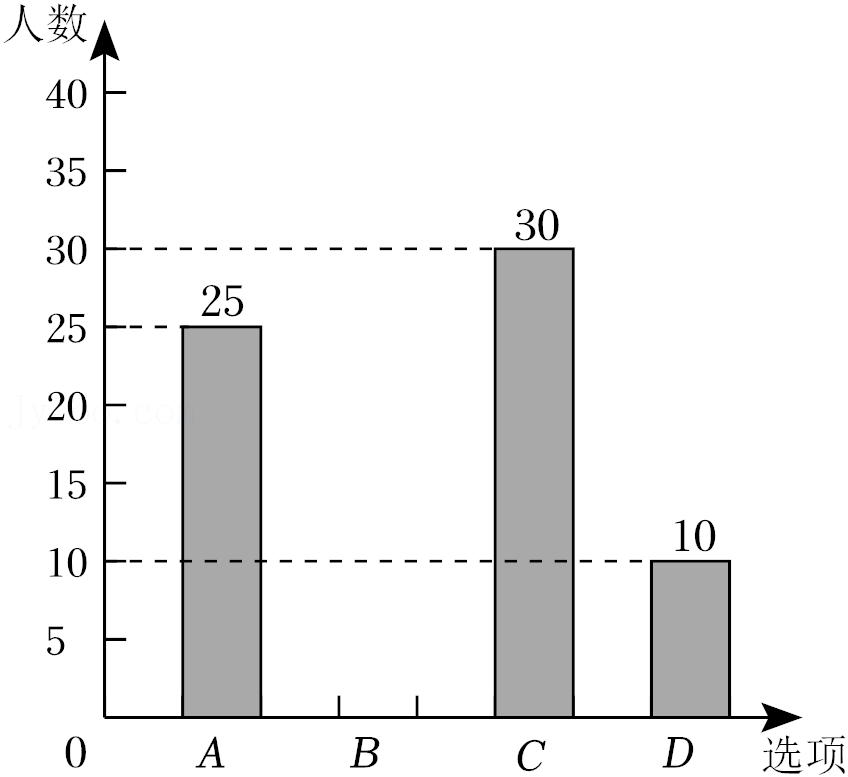
| 项目 | 内容 | 百分比 |
| A | 跳长绳 | 25% |
| B | 抛绣球 | 35% |
| C | 拔河 | 30% |
| D | 跳竹竿舞 | a |
请结合统计图表,回答下列问题:
(1)填空:a= ;
(2)本次调查的学生总人数是多少?
(3)请将条形统计图补充完整;
(4)李红同学准备从抛绣球和跳竹竿舞两个项目中选择一项参加,但她拿不定主意,请你结合调查统计结果给她一些合理化建议进行选择.

23.今年,某市举办了一届主题为“强国复兴有我”的中小学课本剧比赛.某队伍为参赛需租用一批服装,经了解,在甲商店租用服装比在乙商店租用服装每套多10元,用500元在甲商店租用服装的数量与用400元在乙商店租用服装的数量相等.
(1)求在甲,乙两个商店租用的服装每套各多少元?
(2)若租用10套以上服装,甲商店给以每套九折优惠.该参赛队伍准备租用20套服装,请问在哪家商店租用服装的费用较少,并说明理由.
(1)求在甲,乙两个商店租用的服装每套各多少元?
(2)若租用10套以上服装,甲商店给以每套九折优惠.该参赛队伍准备租用20套服装,请问在哪家商店租用服装的费用较少,并说明理由.
24.如图,AB是⊙O的直径,点C是圆上的一点,CD⊥AD于点D,AD交⊙O于点F,连接AC,若AC平分∠DAB,过点F作FG⊥AB于点G交AC于点H.
(1)求证:CD是⊙O的切线;
(2)延长AB和DC交于点E,若AE=4BE,求cos∠DAB的值;
(3)在(2)的条件下,求
的值.
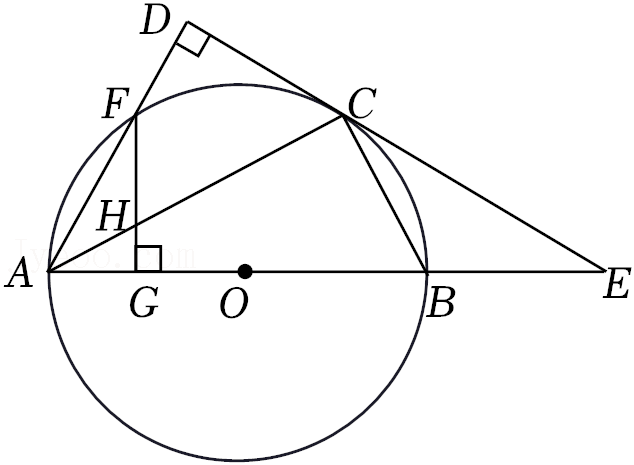
(1)求证:CD是⊙O的切线;
(2)延长AB和DC交于点E,若AE=4BE,求cos∠DAB的值;
(3)在(2)的条件下,求
| FH |
| AF |

25.如图,抛物线y=-x2+3x+4与x轴交于A,B两点(点A位于点B的左侧),与y轴交于C点,抛物线的对称轴l与x轴交于点N,长为1的线段PQ(点P位于点Q的上方)在x轴上方的抛物线对称轴上运动.
(1)直接写出A,B,C三点的坐标;
(2)求CP+PQ+QB的最小值;
(3)过点P作PM⊥y轴于点M,当△CPM和△QBN相似时,求点Q的坐标.

(1)直接写出A,B,C三点的坐标;
(2)求CP+PQ+QB的最小值;
(3)过点P作PM⊥y轴于点M,当△CPM和△QBN相似时,求点Q的坐标.

查看全部题目