下载高清试卷
【2020年浙江省湖州市中考数学试卷】-第1页
试卷格式:2020年浙江省湖州市中考数学试卷.PDF
试卷热词:最新试卷、2020年、浙江试卷、湖州市试卷、数学试卷、九年级试卷、中考试卷、初中试卷
扫码查看解析
试卷题目
1.数4的算术平方根是( )
- A. 2
- B. -2
- C. ±2
- D. √2
2.近几年来,我国经济规模不断扩大,综合国力显著增强.2019年我国国内生产总值约991000亿元,则数991000用科学记数法可表示为( )
- A. 991×103
- B. 99.1×104
- C. 9.91×105
- D. 9.91×106
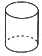
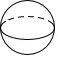
3.已知某几何体的三视图如图所示,则该几何体可能是( )
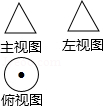

- A.
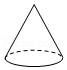
- B.
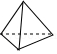
- C.
- D.
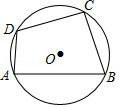
4.如图,已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是( )

- A. 70°
- B. 110°
- C. 130°
- D. 140°
5.数据-1,0,3,4,4的平均数是( )
- A. 4
- B. 3
- C. 2.5
- D. 2
6.已知关于x的一元二次方程x2+bx-1=0,则下列关于该方程根的判断,正确的是( )
- A. 有两个不相等的实数根
- B. 有两个相等的实数根
- C. 没有实数根
- D. 实数根的个数与实数b的取值有关
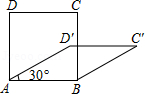
7.四边形具有不稳定性,对于四条边长确定的四边形.当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′.若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )

- A. 1
- B.
1 2 - C. √2
2 - D. √3
2
8.已知在平面直角坐标系xOy中,直线y=2x+2和直线y=
x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
| 2 |
| 3 |
- A. y=x+2
- B. y=√2x+2
- C. y=4x+2
- D. y=x+2
2 √33
9.如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D.则下列结论中错误的是( )
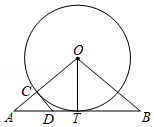

- A. DC=DT
- B. AD=√2DT
- C. BD=BO
- D. 2OC=5AC
10.七巧板是我国祖先的一项卓越创造,流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板,如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形,则这两个图形中,中国七巧板和日本七巧板能拼成的个数分别是( )
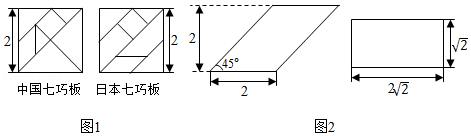

- A. 1和1
- B. 1和2
- C. 2和1
- D. 2和2
11.计算:-2-1= .
12.化简:
= .
| x+1 |
| x2+2x+1 |
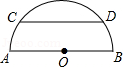
13.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是 .

14.在一个布袋里放有1个白球和2个红球,它们除颜色外其余都相同,从布袋里摸出1个球,记下颜色后放回,搅匀,再摸出1个球.将2个红球分别记为红Ⅰ,红Ⅱ,两次摸球的所有可能的结果如表所示,
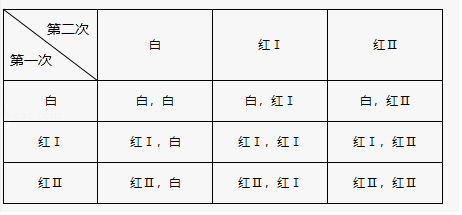
则两次摸出的球都是红球的概率是 .

则两次摸出的球都是红球的概率是 .
15.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点,顶点都是格点的三角形称为格点三角形.如图,已知Rt△ABC是6×6网格图形中的格点三角形,则该图中所有与Rt△ABC相似的格点三角形中.面积最大的三角形的斜边长是 .


16.如图,已知在平面直角坐标系xOy中,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限,反比例函数y=
(x>0)的图象经过OA的中点C.交AB于点D,连结CD.若△ACD的面积是2,则k的值是 .
| k |
| x |

17.计算:
√8
+|√2
-1|.18.解不等式组
.
| { |
|
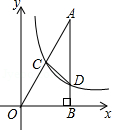
19.有一种升降熨烫台如图1所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.图2是这种升降熨烫台的平面示意图.AB和CD是两根相同长度的活动支撑杆,点O是它们的连接点,OA=OC,h(cm)表示熨烫台的高度.
(1)如图2-1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2-2).求该熨烫台支撑杆AB的长度(结果精确到1cm).
(参考数据:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6)
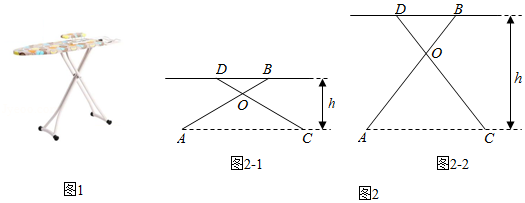
(1)如图2-1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120cm时,两根支撑杆的夹角∠AOC是74°(如图2-2).求该熨烫台支撑杆AB的长度(结果精确到1cm).
(参考数据:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6)

20.为了解学生对网上在线学习效果的满意度,某校设置了:非常满意、满意、基本满意、不满意四个选项,随机抽查了部分学生,要求每名学生都只选其中的一项,并将抽查结果绘制成如图统计图(不完整).
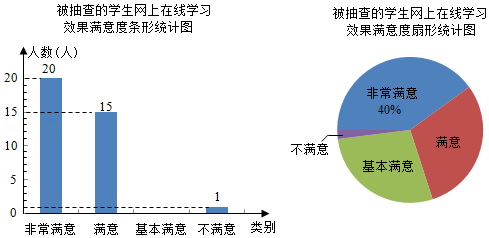
请根据图中信息解答下列问题:
(1)求被抽查的学生人数,并补全条形统计图;(温馨提示:请画在答题卷相对应的图上)
(2)求扇形统计图中表示“满意”的扇形的圆心角度数;
(3)若该校共有1000名学生参与网上在线学习,根据抽查结果,试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人?

请根据图中信息解答下列问题:
(1)求被抽查的学生人数,并补全条形统计图;(温馨提示:请画在答题卷相对应的图上)
(2)求扇形统计图中表示“满意”的扇形的圆心角度数;
(3)若该校共有1000名学生参与网上在线学习,根据抽查结果,试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人?
21.如图,已知△ABC是⊙O的内接三角形,AD是⊙O的直径,连结BD,BC平分∠ABD.
(1)求证:∠CAD=∠ABC;
(2)若AD=6,求⌒CD的长.
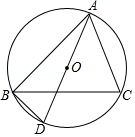
(1)求证:∠CAD=∠ABC;
(2)若AD=6,求⌒CD的长.

22.某企业承接了27000件产品的生产任务,计划安排甲、乙两个车间的共50名工人,合作生产20天完成.已知甲、乙两个车间利用现有设备,工人的工作效率为:甲车间每人每天生产25件,乙车间每人每天生产30件.
(1)求甲、乙两个车间各有多少名工人参与生产?
(2)为了提前完成生产任务,该企业设计了两种方案:
方案一 甲车间租用先进生产设备,工人的工作效率可提高20%,乙车间维持不变.
方案二 乙车间再临时招聘若干名工人(工作效率与原工人相同),甲车间维持不变.
设计的这两种方案,企业完成生产任务的时间相同.
①求乙车间需临时招聘的工人数;
②若甲车间租用设备的租金每天900元,租用期间另需一次性支付运输等费用1500元;乙车间需支付临时招聘的工人每人每天200元.问:从新增加的费用考虑,应选择哪种方案能更节省开支?请说明理由.
(1)求甲、乙两个车间各有多少名工人参与生产?
(2)为了提前完成生产任务,该企业设计了两种方案:
方案一 甲车间租用先进生产设备,工人的工作效率可提高20%,乙车间维持不变.
方案二 乙车间再临时招聘若干名工人(工作效率与原工人相同),甲车间维持不变.
设计的这两种方案,企业完成生产任务的时间相同.
①求乙车间需临时招聘的工人数;
②若甲车间租用设备的租金每天900元,租用期间另需一次性支付运输等费用1500元;乙车间需支付临时招聘的工人每人每天200元.问:从新增加的费用考虑,应选择哪种方案能更节省开支?请说明理由.
23.已知在△ABC中,AC=BC=m,D是AB边上的一点,将∠B沿着过点D的直线折叠,使点B落在AC边的点P处(不与点A,C重合),折痕交BC边于点E.
(1)特例感知 如图1,若∠C=60°,D是AB的中点,求证:AP=
AC;
(2)变式求异 如图2,若∠C=90°,m=6
(3)化归探究 如图3,若m=10,AB=12,且当AD=a时,存在两次不同的折叠,使点B落在AC边上两个不同的位置,请直接写出a的取值范围.
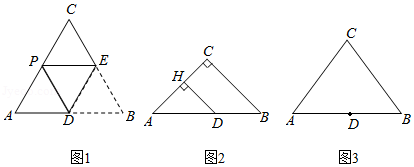
(1)特例感知 如图1,若∠C=60°,D是AB的中点,求证:AP=
| 1 |
| 2 |
(2)变式求异 如图2,若∠C=90°,m=6
√2
,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;(3)化归探究 如图3,若m=10,AB=12,且当AD=a时,存在两次不同的折叠,使点B落在AC边上两个不同的位置,请直接写出a的取值范围.

24.如图,已知在平面直角坐标系xOy中,抛物线y=-x2+bx+c(c>0)的顶点为D,与y轴的交点为C.过点C的直线CA与抛物线交于另一点A(点A在对称轴左侧),点B在AC的延长线上,连结OA,OB,DA和DB.
(1)如图1,当AC∥x轴时,
①已知点A的坐标是(-2,1),求抛物线的解析式;
②若四边形AOBD是平行四边形,求证:b2=4c.
(2)如图2,若b=-2,
=
,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
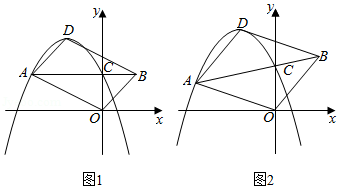
(1)如图1,当AC∥x轴时,
①已知点A的坐标是(-2,1),求抛物线的解析式;
②若四边形AOBD是平行四边形,求证:b2=4c.
(2)如图2,若b=-2,
| BC |
| AC |
| 3 |
| 5 |

查看全部题目