下载高清试卷
【2022年河南省中考数学试卷】-第1页
试卷格式:2022年河南省中考数学试卷.PDF
试卷热词:最新试卷、2022年、河南试卷、数学试卷、九年级试卷、中考试卷、初中试卷
扫码查看解析
试卷题目
1.-
的相反数是( )
| 1 |
| 2 |
- A.
1 2 - B. 2
- C. -2
- D. -
1 2
2.2022年北京冬奥会的奖牌“同心”表达了“天地合•人心同”的中华文化内涵.将这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体中,与“地”字所在面相对的面上的汉字是( )
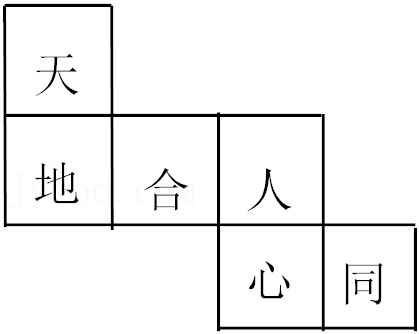

- A. 合
- B. 同
- C. 心
- D. 人
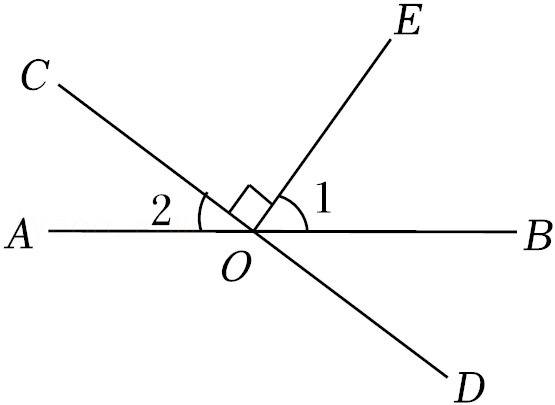
3.如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为( )

- A. 26°
- B. 36°
- C. 44°
- D. 54°
4.下列运算正确的是( )
- A. 2√3-√3=2
- B. (a+1)2=a2+1
- C. (a2)3=a5
- D. 2a2•a=2a3
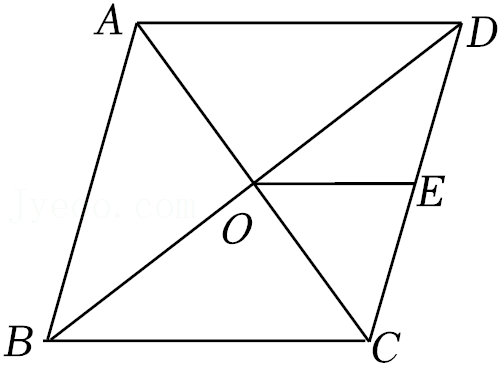
5.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为CD的中点.若OE=3,则菱形ABCD的周长为( )

- A. 6
- B. 12
- C. 24
- D. 48
6.一元二次方程x2+x-1=0的根的情况是( )
- A. 有两个不相等的实数根
- B. 没有实数根
- C. 有两个相等的实数根
- D. 只有一个实数根
7.如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5分),则所打分数的众数为( )


- A. 5分
- B. 4分
- C. 3分
- D. 45%
8.《孙子算经》中记载:“凡大数之法,万万曰亿,万万亿曰兆.”说明了大数之间的关系:1亿=1万×1万,1兆=1万×1万×1亿.则1兆等于( )
- A. 108
- B. 1012
- C. 1016
- D. 1024
9.如图,在平面直角坐标系中,边长为2的正六边形ABCDEF的中心与原点O重合,AB∥x轴,交y轴于点P.将△OAP绕点O顺时针旋转,每次旋转90°,则第2022次旋转结束时,点A的坐标为( )
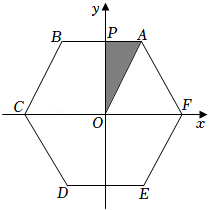

- A. (√3,-1)
- B. (-1,-√3)
- C. (-√3,-1)
- D. (1,√3)
10.呼气式酒精测试仪中装有酒精气体传感器,可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻(图1中的R1),R1的阻值随呼气酒精浓度K的变化而变化(如图2),血液酒精浓度M与呼气酒精浓度K的关系见图3.下列说法不正确的是( )
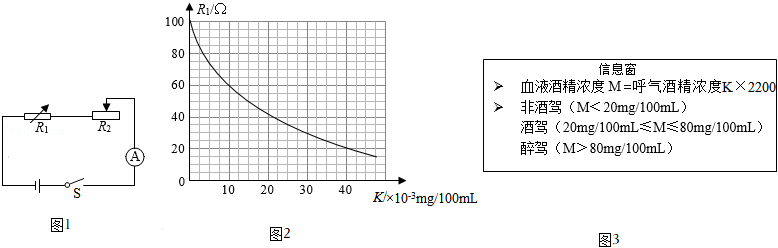

- A. 呼气酒精浓度K越大,R1的阻值越小
- B. 当K=0时,R1的阻值为100
- C. 当K=10时,该驾驶员为非酒驾状态
- D. 当R1=20时,该驾驶员为醉驾状态
11.请写出一个y随x的增大而增大的一次函数的表达式: .
12.不等式组
的解集为 .
| { |
|
13.为开展“喜迎二十大、永远跟党走、奋进新征程”主题教育宣讲活动,某单位从甲、乙、丙、丁四名宣讲员中随机选取两名进行宣讲,则恰好选中甲和丙的概率为 .
14.如图,将扇形AOB沿OB方向平移,使点O移到OB的中点O′处,得到扇形A′O′B′.若∠O=90°,OA=2,则阴影部分的面积为 .
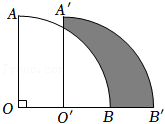

15.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2
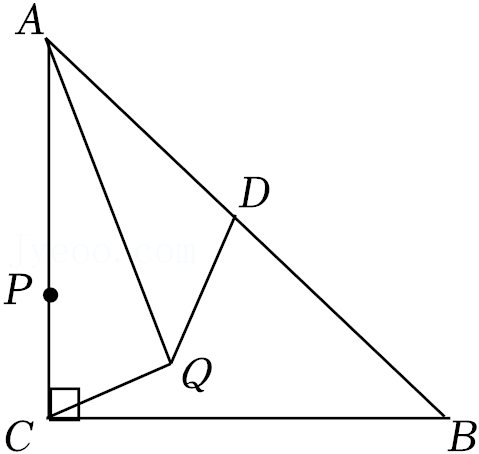
√2
,点D为AB的中点,点P在AC上,且CP=1,将CP绕点C在平面内旋转,点P的对应点为点Q,连接AQ,DQ.当∠ADQ=90°时,AQ的长为 .
16.(1)计算:
)0+2-1;
(2)化简:
÷(1-
).
3√27
-(| 1 |
| 3 |
(2)化简:
| x2-1 |
| x |
| 1 |
| x |
17.2022年3月23日下午,“天宫课堂”第二课在中国空间站开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富相互配合进行授课,这是中国空间站的第二次太空授课,被许多中小学生称为“最牛网课”.某中学为了解学生对“航空航天知识”的掌握情况,随机抽取50名学生进行测试,并对成绩(百分制)进行整理,信息如下:
a.成绩频数分布表:
b.成绩在70≤x<80这一组的是(单位:分):
70 71 72 72 74 77 78 78 78 79 79 79
根据以上信息,回答下列问题:
(1)在这次测试中,成绩的中位数是 分,成绩不低于80分的人数占测试人数的百分比为 .
(2)这次测试成绩的平均数是76.4分,甲的测试成绩是77分.乙说:“甲的成绩高于平均数,所以甲的成绩高于一半学生的成绩.”你认为乙的说法正确吗?请说明理由.
(3)请对该校学生“航空航天知识”的掌握情况作出合理的评价.
a.成绩频数分布表:
| 成绩x(分) | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
| 频数 | 7 | 9 | 12 | 16 | 6 |
b.成绩在70≤x<80这一组的是(单位:分):
70 71 72 72 74 77 78 78 78 79 79 79
根据以上信息,回答下列问题:
(1)在这次测试中,成绩的中位数是 分,成绩不低于80分的人数占测试人数的百分比为 .
(2)这次测试成绩的平均数是76.4分,甲的测试成绩是77分.乙说:“甲的成绩高于平均数,所以甲的成绩高于一半学生的成绩.”你认为乙的说法正确吗?请说明理由.
(3)请对该校学生“航空航天知识”的掌握情况作出合理的评价.
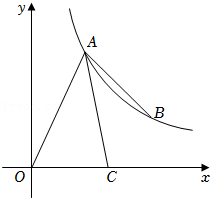
18.如图,反比例函数y=
(x>0)的图象经过点A(2,4)和点B,点B在点A的下方,AC平分∠OAB,交x轴于点C.
(1)求反比例函数的表达式.
(2)请用无刻度的直尺和圆规作出线段AC的垂直平分线.(要求:不写作法,保留作图痕迹)
(3)线段OA与(2)中所作的垂直平分线相交于点D,连接CD.求证:CD∥AB.
| k |
| x |
(1)求反比例函数的表达式.
(2)请用无刻度的直尺和圆规作出线段AC的垂直平分线.(要求:不写作法,保留作图痕迹)
(3)线段OA与(2)中所作的垂直平分线相交于点D,连接CD.求证:CD∥AB.

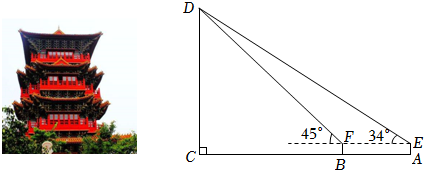
19.开封清明上河园是依照北宋著名画家张择端的《清明上河图》建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁DC的高度,如图,在A处用测角仪测得拂云阁顶端D的仰角为34°,沿AC方向前进15m到达B处,又测得拂云阁顶端D的仰角为45°.已知测角仪的高度为1.5m,测量点A,B与拂云阁DC的底部C在同一水平线上,求拂云阁DC的高度(结果精确到1m.参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67).

20.近日,教育部印发《义务教育课程方案》和课程标准(2022年版),将劳动从原来的综合实践活动课程中独立出来.某中学为了让学生体验农耕劳动,开辟了一处耕种园,需要采购一批菜苗开展种植活动.据了解,市场上每捆A种菜苗的价格是菜苗基地的
倍,用300元在市场上购买的A种菜苗比在菜苗基地购买的少3捆.
(1)求菜苗基地每捆A种菜苗的价格.
(2)菜苗基地每捆B种菜苗的价格是30元.学校决定在菜苗基地购买A,B两种菜苗共100捆,且A种菜苗的捆数不超过B种菜苗的捆数.菜苗基地为支持该校活动,对A,B两种菜苗均提供九折优惠.求本次购买最少花费多少钱.
| 5 |
| 4 |
(1)求菜苗基地每捆A种菜苗的价格.
(2)菜苗基地每捆B种菜苗的价格是30元.学校决定在菜苗基地购买A,B两种菜苗共100捆,且A种菜苗的捆数不超过B种菜苗的捆数.菜苗基地为支持该校活动,对A,B两种菜苗均提供九折优惠.求本次购买最少花费多少钱.
21.小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头P距地面0.7m,水柱在距喷水头P水平距离5m处达到最高,最高点距地面3.2m;建立如图所示的平面直角坐标系,并设抛物线的表达式为y=a(x-h)2+k,其中x(m)是水柱距喷水头的水平距离,y(m)是水柱距地面的高度.
(1)求抛物线的表达式.
(2)爸爸站在水柱正下方,且距喷水头P水平距离3m.身高1.6m的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.

(1)求抛物线的表达式.
(2)爸爸站在水柱正下方,且距喷水头P水平距离3m.身高1.6m的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.

22.为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环⊙O与水平地面相切于点C,推杆AB与铅垂线AD的夹角为∠BAD,点O,A,B,C,D在同一平面内.当推杆AB与铁环⊙O相切于点B时,手上的力量通过切点B传递到铁环上,会有较好的启动效果.
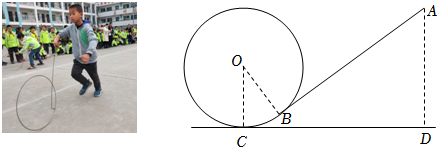
(1)求证:∠BOC+∠BAD=90°.
(2)实践中发现,切点B只有在铁环上一定区域内时,才能保证铁环平稳启动.图中点B是该区域内最低位置,此时点A距地面的距离AD最小,测得cos∠BAD=
.已知铁环⊙O的半径为25cm,推杆AB的长为75cm,求此时AD的长.

(1)求证:∠BOC+∠BAD=90°.
(2)实践中发现,切点B只有在铁环上一定区域内时,才能保证铁环平稳启动.图中点B是该区域内最低位置,此时点A距地面的距离AD最小,测得cos∠BAD=
| 3 |
| 5 |
23.综合与实践
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
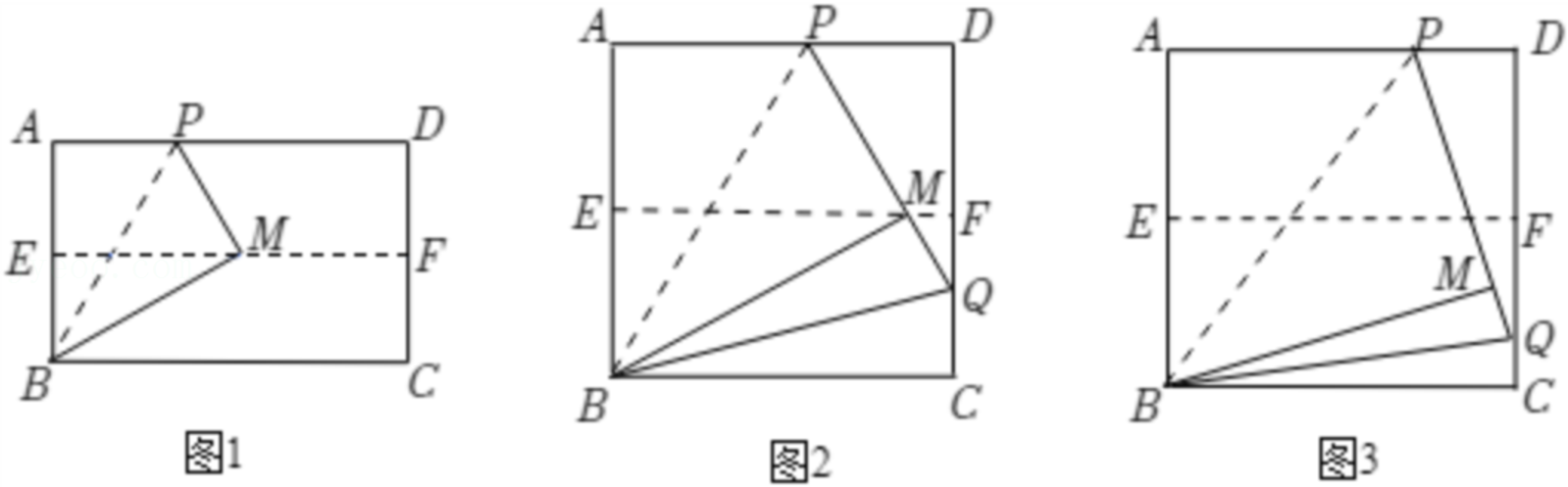
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中一个30°的角: .
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ= °,∠CBQ= °;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,直接写出AP的长.
综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平;
操作二:在AD上选一点P,沿BP折叠,使点A落在矩形内部点M处,把纸片展平,连接PM,BM.
根据以上操作,当点M在EF上时,写出图1中一个30°的角: .
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下:
将正方形纸片ABCD按照(1)中的方式操作,并延长PM交CD于点Q,连接BQ.
①如图2,当点M在EF上时,∠MBQ= °,∠CBQ= °;
②改变点P在AD上的位置(点P不与点A,D重合),如图3,判断∠MBQ与∠CBQ的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片ABCD的边长为8cm,当FQ=1cm时,直接写出AP的长.

查看全部题目