下载高清试卷
【2021-2022学年北京师大附属实验中学七年级(下)期中数学试卷】-第1页
试卷格式:2021-2022学年北京师大附属实验中学七年级(下)期中数学试卷.PDF
试卷热词:最新试卷、2022年、北京试卷、西城区试卷、数学试卷、七年级下学期试卷、期中试卷、初中试卷

扫码查看解析
试卷题目
1.在实数-1,-
中,最小的实数是( )
√3
,0,| 1 |
| 5 |
- A. -1
- B. -√3
- C. 0
- D.
1 5
2.如图,能判定EB∥AC的条件是( )
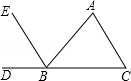

- A. ∠C=∠ABE
- B. ∠A=∠EBD
- C. ∠C=∠ABC
- D. ∠A=∠ABE
3.下列说法中,正确的是( )
- A. ±3是(-3)2的算术平方根
- B. -3是(-3)2的算术平方根
- C. √81的平方根是-3
- D. -3是√81的一个平方根
4.在平面直角坐标系中,点P(0,-4)在( )
- A. x轴上
- B. y轴上
- C. 第三象限内
- D. 第一、三象限的角平分线上
5.二元一次方程组
的解是( )
| { |
|
- A.
{ x=1 y=3 - B.
{ x=3 y=1 - C.
{ x=1 y=0 - D.
{ x=2 y= 1 2
6.下列命题中,假命题是( )
- A. 同旁内角互补,两直线平行
- B. 在同一平面内,过一点有且只有一条直线与已知直线垂直
- C. 如果两个角互补,那么这两个角一个是锐角,一个是钝角
- D. 在同一平面内,如果a∥b,a⊥c,那么b⊥c
7.若
是关于x、y的方程2x-y+2a=0的一个解,则常数a为( )
| { |
|
- A. 1
- B. 2
- C. 3
- D. 4
8.对任意两个实数a、b定义两种运算:a▲b=
,a▼b=
并且定义运算顺序仍然是先做括号内的,例如(-2)▲3=3、(-2)▼3=-2、((-2)▲3))▼2=2,那么(
| { |
|
| { |
|
√5
▲2)▼3√27
等于( )- A. √5
- B. 3
- C. 6
- D. 3√5
9.在某个电影院里,如果用(3,13)表示3排13号,那么2排7号可以表示为 .
10.若x2=4,则x= .
11.如果二元一次方程组
的解为
,则“☆”表上的数为 .
| { |
|
| { |
|
12.已知点P(m,6)在第二象限内,则m的值可以是(写出一个即可) .
13.将一副三角板和一个直尺按如图所示的位置摆放,则∠1的度数为 度.
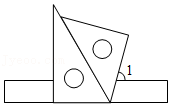

14.有一个无理数生成器,原理如图,当输入的x为729时,输出的y是 .


15.将点P(-2,1)先向右平移2个单位,再向上平移1个单位后,则平移后点P的坐标是 .
16.为了传承中华文化,激发学生的爱国情怀,提高学生的文学素养,七年级举办了“古诗词”大赛,现有小刚、小强、小敏三位同学进入了最后冠军的角逐,规定:每轮分别决出第1,2,3名(没有并列),对应名次的得分都分别为a,b,c(a>b>c且a,b,c均为正整数),选手最后得分为各轮得分之和,得分最高者为冠军,如下表是三位选手在每轮比赛中的部分得分情况,小敏同学第三轮的得分为 分.
| 第一轮 | 第二轮 | 第三轮 | 第四轮 | 第五轮 | 第六轮 | 最后得分 | |
| 小刚 | a | a | 24 | ||||
| 小强 | a | b | c | 13 | |||
| 小敏 | c | b | 11 |
17.计算:
(1)
(2)2(
(1)
√4
+√25
-√100
;(2)2(
√3
-1)+|√3
-2|+3√-64
.18.求下列各式中的x值:
(1)x2-1=
;
(2)3(x-4)3=-375.
(1)x2-1=
| 5 |
| 4 |
(2)3(x-4)3=-375.
19.解下列方程组:
(1)
(用代入法);
(2)
.
(1)
| { |
|
(2)
| { |
|
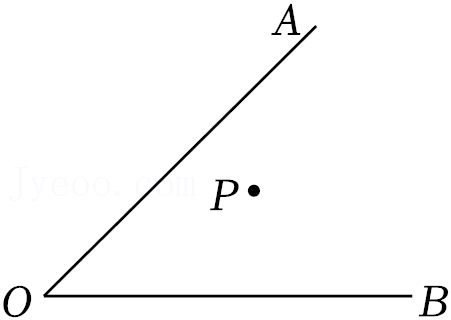
20.已知:∠AOB及∠AOB内部一点P.
(1)过点P画直线PC∥OA交OB于点C;
(2)过点P画线段PD⊥OB于点D;
(3)比较线段PC与PD的大小是 ,其依据是 .
(1)过点P画直线PC∥OA交OB于点C;
(2)过点P画线段PD⊥OB于点D;
(3)比较线段PC与PD的大小是 ,其依据是 .

21.如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和直尺,完成下列各题:
(1)补全△A′B′C′;
(2)连接AA′,BB′,则这两条线段之间的关系是 .
(3)在BB'上画出一点Q,使得△BCQ与△ABC的面积相等.

(1)补全△A′B′C′;
(2)连接AA′,BB′,则这两条线段之间的关系是 .
(3)在BB'上画出一点Q,使得△BCQ与△ABC的面积相等.

22.如图,AB∥CD,∠A=70°,∠2=35°,求∠1的度数.
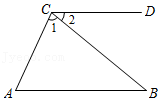

23.下表是某超市两次按原价销售牛奶和咖啡的记录单:
(1)求牛奶与咖啡每箱原价分别为多少元?
(2)某公司后勤部去采购,发现该超市有一部分商品因保质期临近,正在进行打六折的促销活动,于是后勤部决定采购原价或打折的咖啡和牛奶若干箱,其中采购的打折牛奶箱数是采购总箱数的
,最后一共花费1860元,请问此次按原价采购的咖啡有多少箱?
| 牛奶(箱) | 咖啡(箱) | 销售金额(元) | |
| 第一次 | 30 | 10 | 1400 |
| 第二次 | 10 | 20 | 1300 |
(1)求牛奶与咖啡每箱原价分别为多少元?
(2)某公司后勤部去采购,发现该超市有一部分商品因保质期临近,正在进行打六折的促销活动,于是后勤部决定采购原价或打折的咖啡和牛奶若干箱,其中采购的打折牛奶箱数是采购总箱数的
| 1 |
| 4 |
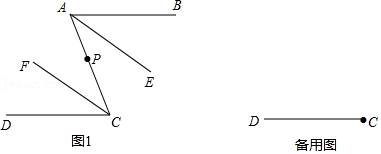
24.已知:射线AB∥射线CD,点P是平面内一点,连接PA,PC,射线AE平分∠PAB,射线CF平分∠PCD
(1)如图1,若点P在线段AC上,求证:AE∥CF;
(2)若点P在射线AB所在直线的上方,且射线AE所在的直线与射线CF所在的直线相交于点Q.直接用等式表示∠APC与∠AQC的数量关系 .
(1)如图1,若点P在线段AC上,求证:AE∥CF;
(2)若点P在射线AB所在直线的上方,且射线AE所在的直线与射线CF所在的直线相交于点Q.直接用等式表示∠APC与∠AQC的数量关系 .

25.设a、b、c都是实数,且
√a+b-6
+|b+c+5|=0,求代数式3a+b-2c的值.26.对于任何实数a,可用[a]表示不超过a的最大整数,即整数部分,{a}表示a的小数部分.例如:[1.3]=1,{-2.6}=0.4.
(1)[
(2)在平面直角坐标系中,有一序列点P1([1],{1}),P2([
请根据这个规律解决下列问题:
①点P10的坐标是 ;
②横坐标为10的点共有 个;
③在前2022个点中,纵坐标相等的点共有 个,并求出这些点的横坐标之和 .
(1)[
√2
]= ,{-√3
}= ;(2)在平面直角坐标系中,有一序列点P1([1],{1}),P2([
√2
],{√2
}),P3([√3
],{√3
}),P4([2],{2}),P5([√5
],{√5
}),…请根据这个规律解决下列问题:
①点P10的坐标是 ;
②横坐标为10的点共有 个;
③在前2022个点中,纵坐标相等的点共有 个,并求出这些点的横坐标之和 .
27.对于平面直角坐标系xOy中的点P(x,y),若点Q的坐标为(x-ky,kx-y)(其中k为常数,且k≠0),则称Q是点P的“k系联动点”,例如:点(1,2)的“3系联动点”的坐标为(-5,1).
(1)点(3,0)的“2系联动点”的坐标为 ;若点P的“-2系联动点”的坐标是(-3,0),则点P的坐标为 ;
(2)设点P(x,y)的“k系联动点”与“-k系联动点”分别为点M,N,若线段MN∥x轴,则点P的位置分布在________,请证明这个结论;
(3)在(2)的条件下,若MN的长度为OP的长度的3倍,求k的值.
(1)点(3,0)的“2系联动点”的坐标为 ;若点P的“-2系联动点”的坐标是(-3,0),则点P的坐标为 ;
(2)设点P(x,y)的“k系联动点”与“-k系联动点”分别为点M,N,若线段MN∥x轴,则点P的位置分布在________,请证明这个结论;
(3)在(2)的条件下,若MN的长度为OP的长度的3倍,求k的值.
查看全部题目
相关试卷推荐
更多热门试卷
如何查看答案以及解析
扫描右侧二维码查看试卷答案解析以及视频讲解