下载高清试卷
【2021-2022学年北京市101中学七年级(下)期中数学试卷】-第1页
试卷格式:2021-2022学年北京市101中学七年级(下)期中数学试卷.PDF
试卷热词:最新试卷、2022年、北京试卷、海淀区试卷、数学试卷、七年级下学期试卷、期中试卷、初中试卷
扫码查看解析
试卷题目
1.4的算术平方根是( )
- A. ±2
- B. ±√2
- C. -2
- D. 2
2.在平面直角坐标系中,点P(3,2)在( )
- A. 第一象限
- B. 第二象限
- C. 第三象限
- D. 第四象限
3.在实数
中,无理数是( )
√2
,√9
,3.1415,| 23 |
| 7 |
- A. √2
- B. √9
- C. 3.1415
- D.
23 7
4.下面四个图形中,∠1与∠2是对顶角的是( )
- A.
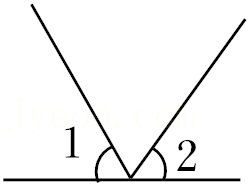
- B.
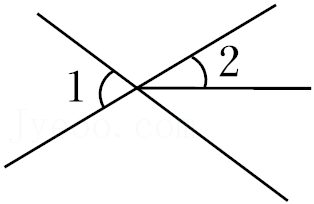
- C.
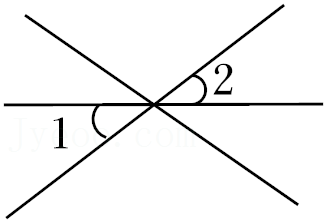
- D.
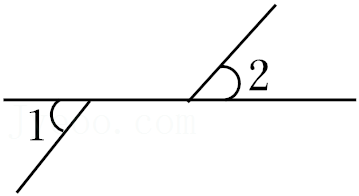
5.在平面直角坐标系中,点B(2,3)到x轴的距离为( )
- A. 3
- B. 2
- C. -3
- D. -2
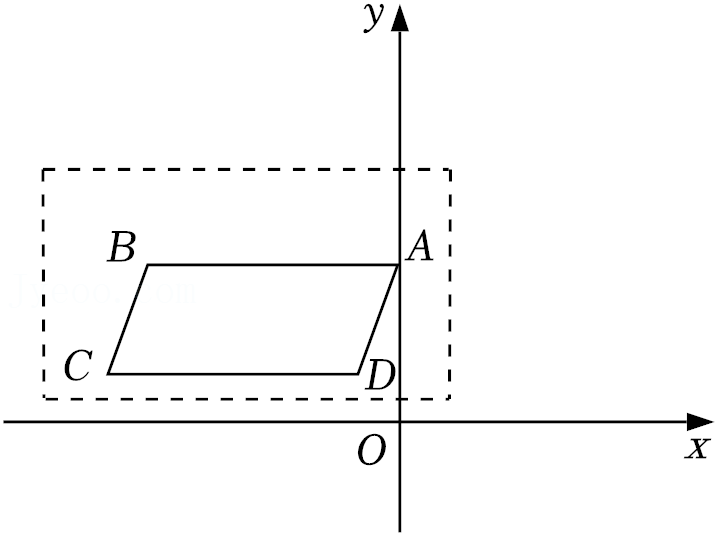
6.在如图所示的平面直角坐标系内,画在透明胶片上的平行四边形ABCD,点A的坐标是(0,2),现将这张胶片平移,使点A落在点A′(3,-1)处,则此平移可以是( )

- A. 向右平移3个单位,再向下平移1个单位
- B. 向右平移3个单位,再向下平移3个单位
- C. 向左平移3个单位,再向下平移1个单位
- D. 向左平移3个单位,再向下平移3个单位
7.估算
√15
的值在( )- A. 6和7之间
- B. 5和6之间
- C. 4和5之间
- D. 3和4之间
8.已知命题:①如果|x|=x,那么x>0;②如果a2=9,那么a=3;③等角的余角相等; ④两个相等的角是对顶角.其中真命题有( )
- A. 1个
- B. 2个
- C. 3个
- D. 4个
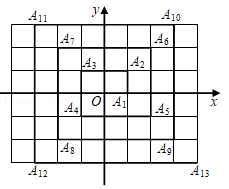
9.如图,A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…按此规律,点A2022的坐标为( )

- A. (505,505)
- B. (506,-505)
- C. (506,506)
- D. (-506,506)
10.在数轴上有三个互不重合的点A,B,C,它们代表的实数分别为a,b,c,下列结论中:
①若abc>0,则A,B,C三点中,至少有一个点在原点右侧;
②若a+b+c=0,则A,B,C三点中,至少有一个点在原点右侧;
③若a+c=2b,则点B为线段AC的中点;
④O为坐标原点且A,B,C均不与O重合,若OB-OC=AB-AC,则bc>0.
所有正确结论的序号是( )
①若abc>0,则A,B,C三点中,至少有一个点在原点右侧;
②若a+b+c=0,则A,B,C三点中,至少有一个点在原点右侧;
③若a+c=2b,则点B为线段AC的中点;
④O为坐标原点且A,B,C均不与O重合,若OB-OC=AB-AC,则bc>0.
所有正确结论的序号是( )
- A. ①②
- B. ③④
- C. ①②③
- D. ①②③④
11.-
√3
的相反数是 ,绝对值是 .12.已知(x-1)2+
√y
=0,则x= ,y= .13.比较大小:
0.5.
√5 -1 |
| 2 |
14.把“内错角相等,两直线平行”改写成“如果…那么…”的形式 .
15.如图,已知线段AB上有两点C,D,且AC:CD:DB=2:3:4,E,F分别为AC,DB的中点,EF=2.4cm,则AB= cm.
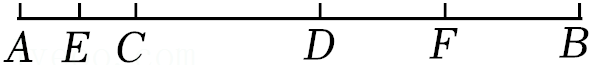
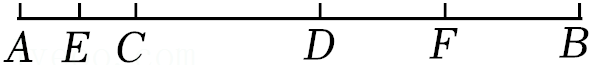
16.小明将一张正方形纸片按如图所示顺序折叠成纸飞机,当机翼展开在同一平面时(机翼间无缝隙),∠AOB的度数是 .


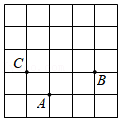
17.已知整点(横纵坐标都是整数)P在平面直角坐标系内做“跳马运动”(即中国象棋“日”字型跳跃).例如:如图,从点A做一次“跳马运动”,可以到点B,但是到达不了点C.设P0做一次跳马运动到点P1,做第二次跳马运动到点P2,做第三次跳马运动到点P3,…,如此依次进行.
(1)若P0(1,0),则P1可能是下列的点 .
D(-1,2);E(-2,0);F(0,2).
(2)已知点P0(4,2),P2(1,3),则点P1的所有可能坐标为 .
(1)若P0(1,0),则P1可能是下列的点 .
D(-1,2);E(-2,0);F(0,2).
(2)已知点P0(4,2),P2(1,3),则点P1的所有可能坐标为 .

18.计算:
(1)
(2)2(
(1)
√16
+3√-27
;(2)2(
√3
+1)+|√3
-2|.19.求出下列等式中x的值:
(1)5x2=35;
(2)
+2=3.
(1)5x2=35;
(2)
| x3 |
| 8 |
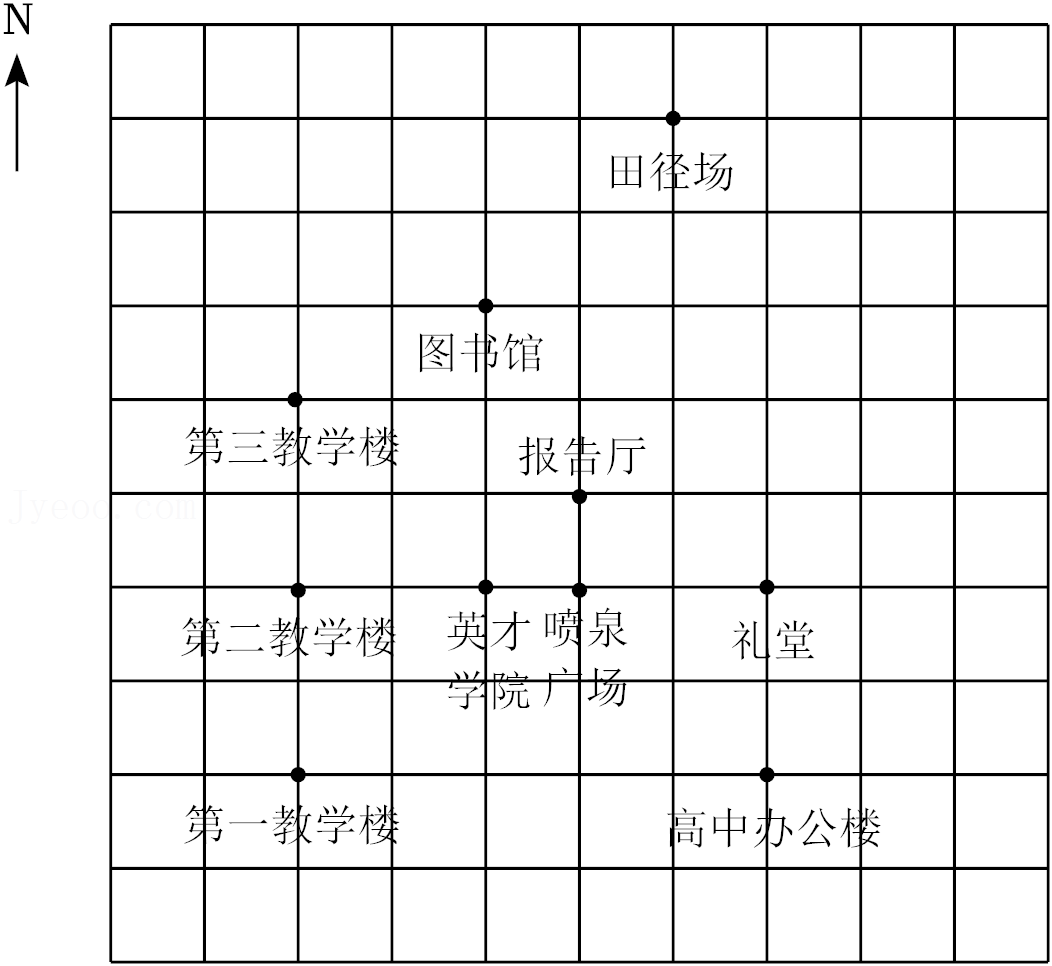
20.如图是一零一校园内一些地点的分布示意图,在图中,分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系.当表示礼堂的点的坐标为(2,0),表示第三教学楼的点的坐标为(-3,2)时,在图中画出平面直角坐标系,并写出田径场、图书馆和第一教学楼的坐标.

21.如图,在方格纸中有一条线段AB和一格点P,仅用直尺完成下列问题:
(1)过点P画直线l∥AB;
(2)在方格纸中,有不同于点P的格点M,使△ABM的面积等于△ABP的面积,格点M共有 个;
(3)在线段AB上找一点N,使得AN+PN+BN距离和最小.

(1)过点P画直线l∥AB;
(2)在方格纸中,有不同于点P的格点M,使△ABM的面积等于△ABP的面积,格点M共有 个;
(3)在线段AB上找一点N,使得AN+PN+BN距离和最小.

22.若实数a+9的一个平方根是-5,2b-a的立方根是-2,求
√a
+√b
.23.完成下面的证明过程:
已知:如图,∠D=120°,∠EFD=60°,∠1=∠2,求证:∠3=∠B.
证明:∵∠D=120°,∠EFD=60° (已知)
∴∠D+∠EFD=180°
∴AD∥EF ( )
又∵∠1=∠2 (已知)
∴ ∥BC (内错角相等,两直线平行)
∴EF∥BC ( )
∴∠3=∠B ( )
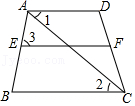
已知:如图,∠D=120°,∠EFD=60°,∠1=∠2,求证:∠3=∠B.
证明:∵∠D=120°,∠EFD=60° (已知)
∴∠D+∠EFD=180°
∴AD∥EF ( )
又∵∠1=∠2 (已知)
∴ ∥BC (内错角相等,两直线平行)
∴EF∥BC ( )
∴∠3=∠B ( )

24.如图,直线AB和CD相交于点O,OD平分∠BOF,OE⊥CD于点O,∠AOC=40°,求∠EOF的度数.

25.如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别相交于C,D两点,记∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,点P在线段AB上.
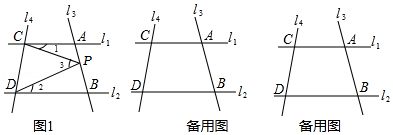
(1)用等式表示∠1,∠2,∠3之间的等量关系,并证明;
(2)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的等量关系(点P和A,B两点不重合),直接写出结论.

(1)用等式表示∠1,∠2,∠3之间的等量关系,并证明;
(2)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的等量关系(点P和A,B两点不重合),直接写出结论.
26.材料1:两数和的完全平方公式:两个数的和的平方,等于它们的平方和,加上它们的积的2倍,即(a+b)2=a2+2ab+b2,比如(x+6)2=x2+2•x•6+62=x2+12x+36.
材料2:学习了无理数后,某数学兴趣小组开展了一次探究活动:估算
∵
∴13=9+6k+k2,∴13≈9+6k,解得k≈
,∴
≈3.67.
(1)请你结合材料1和材料2,估算
(2)请结合上述具体实例,概括出估算
材料2:学习了无理数后,某数学兴趣小组开展了一次探究活动:估算
√13
的近似值.小明的方法:∵
√9
<√13
<√16
,设√13
=3+k(0<k<1),∴(√13
)2=(3+k)2,∴13=9+6k+k2,∴13≈9+6k,解得k≈
| 4 |
| 6 |
√13
≈3+| 4 |
| 6 |
(1)请你结合材料1和材料2,估算
√37
的值(写过程,结果保留两位小数).(2)请结合上述具体实例,概括出估算
√m
的公式:已知非负整数a,b,m,若a<√m
<a+1,且m=a2+b,则√m
≈ .(用含a,b的代数式表示)27.我们学习过角的定义,有公共顶点的两条射线组成的图形叫做角.如图所示,我们把区域Ⅰ(不包括射线OM和射线OA)叫做角的内部.

对于一个角α(0°<α<180°且a≠90°),定义它的“内补角”满足以下两个条件:
①大小是180°-α;②与这个角有一条公共边且与这个角的内部有公共部分.
定义它的“内余角”满足以下两个条件;
①大小是|90°-α|;②与这个角有一条公共边且与这个角的内部有公共部分.
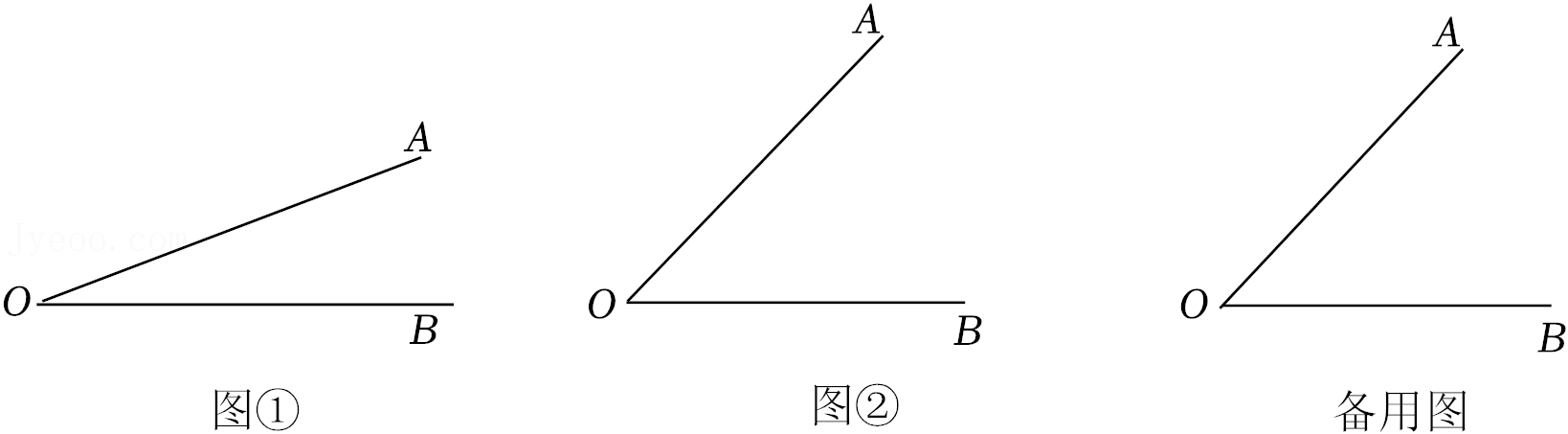
(1)如图①,已知∠AOB=20°,利用直尺和量角器,通过计算和测量,作出∠AOB的所有的内补角;
(2)设∠AOB=α,射线OM平分∠AOB的内补角,射线ON平分∠AOB的内余角,
①当α=45°时,如图②,计算∠MON的大小为 ;(直接写答案)
②当90°<α<135°时,∠MON大小为 .(用含α的代数式表示,直接写答案)

对于一个角α(0°<α<180°且a≠90°),定义它的“内补角”满足以下两个条件:
①大小是180°-α;②与这个角有一条公共边且与这个角的内部有公共部分.
定义它的“内余角”满足以下两个条件;
①大小是|90°-α|;②与这个角有一条公共边且与这个角的内部有公共部分.
(1)如图①,已知∠AOB=20°,利用直尺和量角器,通过计算和测量,作出∠AOB的所有的内补角;
(2)设∠AOB=α,射线OM平分∠AOB的内补角,射线ON平分∠AOB的内余角,
①当α=45°时,如图②,计算∠MON的大小为 ;(直接写答案)
②当90°<α<135°时,∠MON大小为 .(用含α的代数式表示,直接写答案)

28.在平面直角坐标系xOy中,对于给定的两点P,Q,若存在点M,使得△MPQ(△表示三角形)面积等于1(即S△MPQ=1),则称点M为线段PQ的“单位面积点”.
解答下列问题:
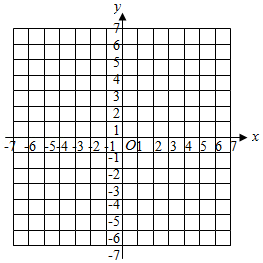
如图,在平面直角坐标系xOy中,点P的坐标为(2,0).
(1)在点A(-1,1),B(-1,2),C(2,-4)中,线段OP的“单位面积点”是 ;
(2)已知点D(0,3),E(0,4),将线段OP沿y轴方向向上平移t(t>0)个单位长度,使得线段DE上存在线段OP的“单位面积点”,求t的取值范围;
(3)已知点F(2,2),点M在第一象限且M的纵坐标是3,点M,N是线段PF的两个“单位面积点”,若S△OMN=3S△PFN,且MN∥PF,直接写出点N的坐标.
解答下列问题:
如图,在平面直角坐标系xOy中,点P的坐标为(2,0).
(1)在点A(-1,1),B(-1,2),C(2,-4)中,线段OP的“单位面积点”是 ;
(2)已知点D(0,3),E(0,4),将线段OP沿y轴方向向上平移t(t>0)个单位长度,使得线段DE上存在线段OP的“单位面积点”,求t的取值范围;
(3)已知点F(2,2),点M在第一象限且M的纵坐标是3,点M,N是线段PF的两个“单位面积点”,若S△OMN=3S△PFN,且MN∥PF,直接写出点N的坐标.

查看全部题目
相关试卷推荐
更多热门试卷
如何查看答案以及解析
扫描右侧二维码查看试卷答案解析以及视频讲解